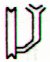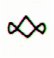With winter solstice close to the end of side a of the Mamari tablet, it would not be strange if side b was the side of the moon.

If we connect the end of side b with the beginning of side a, we have 64 glyphs + 25 = 89 counted beyond mago koti:

	14			63	24
Cb11-17		Cb12-10	Cb12-11 (1)			Ca1-25 (89)

89 implies there must be 453 days from Cb12-11 to manu kake and 456 days to the end of side a:

	87		363		2
Cb12-11 (1)		Ca1-25 (89)		*Ca14-26 (453)		*Ca14-29 (456)
456 = 19 * 24

Using our experience, we can improve this table:

	88		363		1
Cb12-11 (1)		Ca1-25 (90)		*Ca14-26 (454)		*Ca14-28
456 = 19 * 24

14 * 28 = 392, and it should be the last glyph of the front side. The trick is to push *Ca14-29 to the back side and count the last glyph on side b twice:

Cb14-14	Cb14-15	Cb14-16	Cb14-17	Cb14-18	Cb14-19

14 * 14 = 196 = 392 / 2. Cb14-28 will be the last glyph on the back side, and counted from *Ca14-29 it will be number 348 (= 12 * 29).

Rogo at *Ca14-25 is glyph number 363 counted from the 'nut' in Ca1-26:

		362
Ca1-25	Ca1-26		*Ca14-25	*Ca14-26 (364)

Clearly the sun must be the subject on side a. Are there any Rogo glyphs on side b? These are the honu glyphs on side b:

Cb13-24 and Cb14-12 belong to the 'front side', and then 12 honu remain on the 'back side'. After eliminating half of them - glyphs without any sign of Rogo - three pairs are left:

On the 'back side' pairs should be expected.

Our attention is immediately caught by the central pair, holes should imply the time of Rogo has come to an end.

 And at top right prominent signs in form of a double mata must indicate something important. This type of sign we have recently seen at day 360:

Ca13-16	Ca13-17 (360)	Ca13-18	Ca13-19	Ca13-20 (363)
*Ca14-1 (364)	*Ca14-2	*Ca14-3 (366)	*Ca14-4	*Ca14-5 (368)

We must count:

	63	359		7
Cb12-11			Ca13-17 (360)		*Ca14-5 (368)
64 = 8 * 8		360 = 15 * 24		8
432 = 18 * 24

24	127			154
		Cb6-13 (520)	Cb6-13		Cb12-10
152 = 8 * 19			156 = 12 * 13
308 = 11 * 28

Here *Cb14-19 is counted only once. 433 does not seem to carry any significant numerical message.

Counting *Cb14-19 twice will increase the total 740 to 741 = 3 * 13 * 19.

The 8 nights which end with *Ca14-5 (number 368 from Cb12-11) are nights in the dark, nights of Rogo, nights of winter solstice.

The straight downwards sloping arm of tagata at day 360 indicates sun going down, while the pair of non-present Rogo glyphs in the center of side b presumably represent waxing and waning moon. Their stomachs are somewhat like rhombs.

11 * 28 possibly implies 308 nights include 'one more', i.e. the child of next year.

The reason why winter solstice appears twice at the end of side a has now become clear. The first group represents winter solstice from the perspective of the sun:

glyph numbers counted from Ca1-1
Ca13-16	Ca13-17 (360)	Ca13-18	Ca13-19	Ca13-20 (363)
*Ca14-1 (364)	*Ca14-2	*Ca14-3 (366)	*Ca14-4	*Ca14-5 (368)

The second group belong to the 'back side':

*Ca14-6	*Ca14-7	*Ca14-8 (371)
344	345	346
*Ca14-9 (372)	*Ca14-10	*Ca14-11	*Ca14-12	*Ca14-13	*Ca14-14
347	348	349	350	351	352
*Ca14-15 (378)	*Ca14-16	*Ca14-17
353	354	355

*Ca14-15 is exactly the same vero Rogo as in Ca13-19:

Ca13-19	Ca13-20		*Ca14-15	*Ca14-16
362	363		353	354

Counting by the sun the day is 1 day before the turning point (363), counting by the moon it is one day before the last night (354 = 12 * 29.5). The meaning is the same, but the numbers are different.