|
TRANSLATIONS
20 glyphs at the beginning (period 1) of the calendar of the year in E and 26 at the end (period 24). In the midsections of H we have 20 and 6, i.e. the same numbers (20 + 6 = 26) structured differently:
Then we remember 20 and 26 together with 29 in Tahua. Primarily the structure is:
The 'long count' (including Ab7-26 and Aa8-26) - bottom above - measures 26 * 29 = 754 glyphs, the 'short count' (excluding Aa8-26 and Ab7-26) measures 20 * 29 = 580 glyphs. 754 + 580 = 46 * 29 = 1334 = 314 * 4 + 36 + 42 754 = 400 + 354 (where 354 = 12 * 29½) 580 = 300 + 280 (where 280 = 10 * 28) Aa8-26 is at the beginning of the 'short count' (i.e. at left above) and the aberrant top of the glyph suggests Ca7-23:
As if Aa8-26 were a rei miro the glyph appears before side b, which I earlier have concluded is where the reading should start (because Metoro began there and because Ab1-1 is an 'uncontaminated' viri). From the beginning (beyond Aa8-26) we have a 'short count' defined by 20 and 29. Probably 29 is to be regarded as 26 + 3, where 3 are extracalendrical nights. Earlier we have arrived at this suggestion by way of Aa1-13--15:
In period no. 3 of the G calendar we probably have support for this reading, because the 'feathers' around the perimeter of the glyph are arranged as 14 + 3 extra small ones:
Furthermore, there are 3 extra 'toes' (right bottom) which are separated from the rest of the glyph - a sign, I believe, of 'ghostly status' (outside the regular and normal order of things). In the 6th period of G we have another arrangement, with 16 = 10 + 6 feathers:
We should not forget that 180 + 182 = 362 implies a need for 3 extra nights.
The set of basic numbers seems to be: 3 (dark extracalendrical nights), 4 (cardinal points of the earth), 6 (for the flames of the sun, also for the number of solar double-months in a year), 8 (the perfect number, the number of periods in the Mamari moon calendar), 10 (periods before Kuukuu dies), 12 (solar months to reach 360 days), 14 (½ of the 28 moon-lit nights), 16 (½ of the 32 period long cycle in the G calendar), 18 (½ of 360, the nexus which correlates the E and G calendars), 20 (a complete set corresponding to the number of fingers and toes), 24 (3 * 8, i.e. moon = 2 * 12, i.e. sun), 26 (a moon measure: 364 / 14), 28 (number of sun-lit moon nights in a month). The 'short count' 20 * 29 is divided into two parts (3 * 20) and (26 * 20), by Ab1-1 (where the reading of the tablet begins). At left of Ab1-1 the extracalendrical period, shown by 3 (in 3*20 = 60), is located, at right of Ab1-1 the normal seasons begin. Although in the 'short count' period 20 * 29 the viri end points (Aa8-26 and Ab7-26) are not included, the viri which marks where the reading should start (Ab1-1) is located 3 * 20 glyphs beyond Aa8-26 as counted in the normal way. There are two possible ways to count 'normal', either the start glyph is included or the end glyph (but not both). Here we can determine that Aa8-26 should not be included (but Ab1-1 must be included). Because the measure 20 * 26 (the great first phase of the reading) is a 'short count' (neither including Ab1-1 nor Ab7-26). In E there are 20 glyphs in the first period and 26 in the last. I interpret this fact to mean that sun is associated first of all with 20. The natural counting base 20 is a symbol of order and sun gives us the necessary light to see this. 26 is twice 13, which E states by way of 7 + 6 + 7 + 6. When the moon-lit nights are counted we have 14 + 14 = 28. 26 is a measure where sun and moon cooperate. In H we first encounter, in the middle of side a, a group with 20 glyphs and then, immediately afterwards, a group with 6 glyphs. I guess this is to suggest that 26 = 20 + 6, a fact which in E is expressed in a similar way because 7 + 6 + 7 + 6 easily can be read as (7 + 6 + 7) + 6 = 20 + 6. In Tahua the close association between 20 and 26 is expressed by multiplying them: 20 * 26 = 520. We, who are used to count weeks (instead of fortnights) think of 52 weeks here, but I guess the Easter Islanders thought otherwise. Maybe they read 520 as 2 * 26, because in a 'year' there is room for 26 weeks. In any case we should not read 520 = 4 * 13 (as in a deck of cards), because the glyph numbers point at 26 (not at 13). Furthermore 13 is odd. The 'short count' 20 * 29 has at left the 'female' dark (as during new moon) phase. 3 times 20 suggests 3 wives of the sun:
At right arrives the harmonious rule of the sun together with the moon. The 'long count' 26 * 29 = 754 has a darker weight than the 'short count' 26 * 20: 754 = 400 + 354 (where 354 = 12 * 29½) 400 may be read as the 4 quarters of the earth and in 354 is the dark phase of the month (29½ - 28) included. If we read (which is reasonable) 26 * 29 as 26 * 20 + 26 * 9 we notice the evil 9 (not only odd but also a mark of death). I have put the 'long count' 26 * 29 at the bottom of the diagram above, because the dark is below (while sun is above). Yet, we have noticed how sun seems to be shining brightly on side a, at least up to midsummer. Maybe this is to counterbalance the dark aspect of 754? Aa4-72 should be included in our investigation, and also the 4th viri, Aa5-7. To keep the grasp which we now have reached, I add these further complications separately below:
The 'long count' 26 * 29 can be divided into parts, and then number 18 appears between Aa4-72 and Aa5-72 (given that we count 'long', counting 'short' we get 16). Between Ab7-26 and Aa4-72 (i.e. counted 'short') there are 16 * 29 glyphs. Aa4-72 is then connected to Aa5-7 by way of counting 'long', and the measure is 18. Maybe 18 makes a statement about the summer season (360 / 2). Aa5-7, the 4th viri (given that we begin with Aa8-26, move in the same direction as the glyphs, find Ab1-1, later Ab7-26 and at last Aa5-7), is offset (it seems) 18 glyphs away from the location which would have given 10 * 29 glyphs (by counting 'long') to the 1st viri (Aa8-26). Aa4-72 evidently has taken its place. 10 * 29 for the last phase of the cycle must be counted 'long' because Aa8-26 was not counted at the start of the cycle. That means we cannot count 'long' once again to go backwards from Aa5-7 to reach Aa4-72 (because then Aa5-7 would be counted twice). We must count 'short', i.e. to 16.
Red figures are the results of normal counting. They are ugly, not one of them even:
The distribution of short, normal, and long counting modes should be documented clearly:
Here in the north of Sweden we notice how short the days are around winter solstice. At that time it is around summer solstice on Easter Island and the days must be longer than normal. Coordinating seasons with the modes of counting it is evident that the 'short' mode appears in the 'sunny' season. That is exactly as expected, because they counted 'nights' instead of 'days'. The conclusion - although admittedly rather weak - is that the summer season has its place on side a of Tahua, while winter is located on side b. Maybe we should also draw the conclusion that a fully grown viri implies normal counting mode? If we introduce Aa4-72 into the table it becomes more complicated:
16 must be counted short (as is described earlier above). Therefore Aa4-72 must be included in the counting from the 3rd viri and that glyph has not been counted earlier. Therefore the counting must be long, resulting in 466. To introduce Aa4-72 into the table changes the counting mode from normal to long ahead of the 3rd viri. Well, now. All these intricate ideas was just an introduction to what I intended to investigate, viz. if there is some numerical connection between the viri constellation and te pito (Ab8-43):
As we already know, Ab8-43 is located at the beginning of the 2nd half of line b8 (which has 84 glyphs). That means the distance to the 1st viri (Ab8-26) to the left (backwards in time) is 43 - 26 = 17 (counted normally, i.e. from Ab8-27 up to and including Ab8-43). Obviously that is a wrong counting mode (if there is a connection between te pito and the viri), because the result must be even. The 1st viri is already counted (long together with the 4th viri). Therefore there is only one possible counting mode left, viz. short. The result is 16 and we immediately think of Aa4-72. Let us now count the distances (forwards and backwards) between te pito and Aa4-72:
The counting modes become beutifully arranged. The normal counting modes have disappeared and there are regular undulations between short and long. The distances between te pito and Aa4-72 are 44 + 520 + 466 = 1030 respectively 16 + 272 + 16 = 304. Neither number is a multiple of 29. Maybe we should read them as 10-30 respectively as 30-4? Another idea is to divide 304 by 1030. The result is 29.51 % and one comes to think of the possibility of this measure having been created to describe the lunar month, not 29, not 29 ½, but a more precise measure. According to Wikipedia, the synodic month is 29.53 days. How close can you get to that number by the method imagined (division of two numbers less than 1,334)? If we increase from 304 to 306 (we must use only even numbers), 1030 will shrink to 1028 and then we get 29.77 %. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

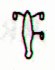



 .
.