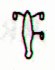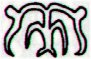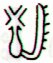A problem is nagging me: I have suggested (under henua ora in the glyph dictionary) that the G calendar has 12 periods for summer:

'... summer in G ends with period no. 12 ...' (and begins with period no. 1)

On the other hand the glyphs tell about a kind of midpoint, probably summer solstice, between periods no. 8 and 9:

8			9
	Ga4-5	Ga4-6		Ga4-7	Ga4-8
	Ka5-2	Ka5-3		Ka5-4	Ka5-5

And in the 15th period the dark season is mentioned:

Counting, we reached the conclusion that 180 + 182 + 3 = 365 probably is the structure in G:

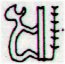
Finally:

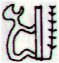
Unquestionably the glyphs before the 17th period should belong to the summer season. Does that mean we should allocate the first 8 glyphs to the 2nd quarter and the 2nd group of 8 glyphs to 3rd quarter? If so, then summer (= the 2nd + the 3rd quarters) would end with the 16th period (not the 12th). This would be in harmony with a 'break' between the 8th and 9th periods.

Let us take a look at the periods up to no. 12. I would like to sort them into two groups with 6 periods in each.

The 2nd of these groups them becomes:

According to Ga3-14 the 3 extracalendrical nights occur at the ultimate end (after the finish of the regular calendar) - symbolized by toes separately drawn.

The beginning of the regular calendar has 2 great 'feathers' and I imagine they may be the two seasons (summer and winter). Then follows 4 powerful 'feathers' which could be the 4 quarters. Then appears 4 small 'feathers', followed by 4 'feathers' of more normal size: 2 - 4 - 4 - 4 -- 3.

Let us compare with the year summary in Tahua:

If in Ga3-14 we disregard the 2 extraordinary great 'feathers' we have 3 tertials in a 12-period year. In Tahua we seem to have tertials too.

In Ga3-22 we have 16 feathers with a more subtle pattern. I guess these refer to the winter season, when the changes are less noticeable. The shark at right also signifies, I think, darkness.

There are many questions to be answered before we have a clear grasp of the G calendar.

The double-headed bird in Ga3-1 (GD58, manu kake) for instance, does it not suggest the summer season? In Keiti we saw two manu kake, presumable one for the winter (fishy bottom) and one for summer (bird bottom):

If Eb5-31 connects to Eb5-30, then it maybe connects also to Eb5-29. If so, then - possibly - the 'fishy' season is divided into 1st quarter + 4th quarter. How else could a complete fishy many kake leave at winter solstice?

Why is there no fishy manu kake in the 1st period of G? Answer (maybe): In G (supposedly) spring is the starting point of the calendar and then a bird manu kake (if leaving) could represent the whole year:

Ga3-2 suggests a little bird looking down at a little henua (the new year?) and Ga3-3 is crowing triumphantly over the dark (dead?) fish (winter). But in Ga3-2 the little bird has ghostly feet. Why?

In Ga3-1 there is a pronounced Y-form in the neck; does it symbolize equinox (the division point between - according to G - old and new year? If so, then there would hardly be room for two manu kake glyphs here. One glyph captures both. In the triplet Eb5-29--31 the hand is communicating Y.

In Ga2-29 the top of the niu has closed 'limbs' (not 'ghostly'). I guess this means the summer season (affirming that the G calendar does not begin at winter solstice). But then, why ghostly limbs on niu in the 7th period of E:

Eb3-20	Eb3-21	Eb3-22	Eb3-23	Eb3-24

Whatever the answers may be to all these questions, one thing is clear - there is much similarity between the general design of period 7 in E and period 1 in G.

PS: The 'fishy' manu kake exists in G too:

These 12 glyphs maybe are connected into a 3-package group of periods. Possibly there are 6 such 3-package groups, together describing the 180 days of summer:

The odd 19 suggests we must add further glyphs until we have added another period with an odd number of glyphs (at which point the sum becomes even). If this assumption is correct, then the periods from 1 up to and including 12 belong together. 42 (= 6 * 7) is a number which affirms that we are on the right track.

The last two 3-package groups add up to 28 (= 4 * 7) glyphs. I.e., the first half year will have (6 + 4) * 7 = 10 * 7 = 70 glyphs = a lunar double-month (= 420 / 6). 35 as sum for the 1st 9 periods indicates half the lunar double-months. Although the table suggests that periods 1-12 belong together, it also suggests that the periods 1-9 belong together. The 'break' between period 8 and 9 could refer to summer solstice and the break between 12 and 13 to the calendrical break between the first quarter and the 2nd (as defined in G - maybe equal to the 2nd and 3rd quarters in E).

The glyphs in period 13 include rei miro (Ga4-17) and signs describing the 24 dark half-month periods. Manu kake with fishy bottom here seems to tell us about what is coming.

If we leave G for the moment and look at the calendar in E, we may start at its beginning and count forward 20 (as suggested by the 20 glyphs in its first period and by our experience from 20 * 29 glyphs in the first long sequence of Tahua). Each period represents half a month, i.e. presumably a fortnight, which means 20 weeks:

Using the clue 20, we can understand why henua ora appears. Metoro, it seems, took a deep breath and coordinated Eb3-38 with Eb4-1 (Capital letter at Te maitaki). He also suddenly changed the order between kiore - henua and it became henua - kiore.

'... From Eb4-1 Metoro furthermore shifted to read the parts of a certain type of glyph from right to left (instead of the correct from left to right). Though Eb4-31, Eb5-24 and Eb6-19 he read correctly (from left to right).'

Eb6-19 is the very last glyph in the calendar and the other two cases are periods nos. 16 and 22:

What happens if we count 26 backwards from period 24?

In normal counting procedure we do not count the spot we stand on. Here, counting backwards, we must count the spot we stand on (i.e. period 24 in our example). Counting normal can be defined as not counting the spot you stand on (but counting the goal spot). Here we ought to have reversed normal counting = counting the spot you stand on but not the goal spot.

However, when we name periods by number we use long counting. We include the spot we stand on (as for example when we numbered period no. 10 as number 10).

When we now will count backwards from period 24 we naturally will count period 24 as the first period. By long counting from 24 we will reach 24 - 26 / 2 + 1 = 11:

11
	Eb4-2	Eb4-3	Eb4-4	Eb4-5	Eb4-6
	te vero	te henua	toko tokoga	te henua - e rima	te kiore - te henua

Very interesting. Eb4-3 is a 'midnight' henua, not suitable for summer. If there is a reversal after 20 weeks (10 periods), then it would not surprise me if it is the pattern of the death of Kuukuu: