Hevelius has the Phoenix constellation at the other end of the sky compared to Crater and we ought to add the Phoenix stars to our list. Below I can count to 23 stars with Greek letters, but I will not bother to regard λ¹ and λ² as separate items: 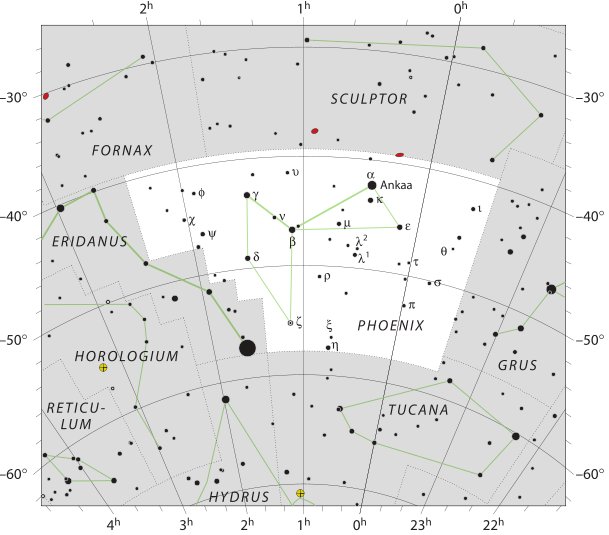
The right ascension positions of the earliest stars in Phoenix are in the 24th hour and therefore not possible to coordinate with the earliest glyphs in the C text. But we can try to add them to the G text. (In K the heliacal stars were probably rising in the interval 5h - 16h.)
There is a dot in front in Gb3-3, where the first Phoenix star (ι) rose heliacally. From March 13 to 0h there are 8 days. I have counted the right ascension days from Rogo in Gb6-26, and when after a full cycle time returns to Gb6-26 the date has changed from March 21 to July 6, moved ahead with 7h:
By adding 7h to 24h the cycle becomes 31h, and because 31 is a prime number it is necessary to 'recycle' 24h for 31 years in order to return to the place of origin. This is the same structure as when 24 hours in a day will accumulate to 24 * 31 = 744 hours in a month like July and August. Perhaps this structure explains why 372 days evidently was an important number. 31 * 12 = 372 days and 12 * 31 (= 744 / 2) could describe the number of daytime hours in a month. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||





