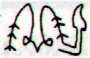TRANSLATIONS

next page previous page up home
 

Next page:

 

It is reasonable to count from winter solstice if ariki is related to the path of the sun, while tamaiti instead apparently is calibrated after the moon. Our featherless ariki is at the end of the 4th month from winter solstice if we cound with 29 nights per month:

114 123
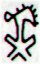Gb6-26 Ga2-21 (52) Ga7-6 (176)
116 = 4 * 29 124 = 4 * 31
240 = 8 * 30

And if we then change 'currency' from dark months (29) to more normal months (31) we will find a beautiful balance with the feathered ariki in Ga7-6 at day number 240 from winter solstice.

Also ariki in Ga6-3 can be found a place in the map, 8 * 26 is 32 less than 8 * 30:

114 3 87 31
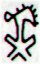Gb6-26 Ga2-21 (52) Ga2-25 Ga6-3 (144) Ga7-6
1 116 = 4 * 29 120 208 = 8 * 26 240
240 = 8 * 30

And, we can imagine another pattern too, viz. that honu in Gb6-26 relates to the featherless ariki in Ga2-21, while the feathered ariki in Ga6-3 and Ga7-6 in a similar way relate to the strange Ga2-25. The rounded 'body' in Ga2-25 resembles that in Gb6-26.

Yes, we can go even farther, and search for day 360:

118 118 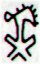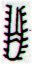118
Gb6-26 Ga2-25 (56) Ga2-26 Ga7-6 (176) Ga7-7 Gb3-5 (296)
1 120 121 240 241 360

The triplet of 118 (= 4 * 29.5) is a result of the pattern with 120 days (given that we show both the first and last glyphs in a period).

One feathered ariki remains to explain:

20
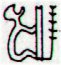
Ga5-22 Ga5-23 Ga5-24 (135) Ga5-25
Ga5-26 Ga5-27 Ga5-28 Ga5-29

135 - 52 (at Ga2-21) = 83, and 116 + 83 = 199, which means the fat honu in Ga5-25 will be number 200. Darkness is increasing it says in Ga5-27. When waning is beginning there should be a fat 'person', and here he is in day 200. But his rounded figure can also allude to Gb6-26 and Ga2-25.

We have now investigated all but three of the ariki glyphs in G:

Ga1-5 Ga1-13 Ga1-24 Ga2-21 Ga5-24 Ga6-3 Ga7-6
Gb3-7 Gb7-11

These we leave until later speculations. We can therefore conclude here by drawing attention to the top left limb in Ga2-21 and the top right limb in Ga7-6, we can guess the meaning - Ga2-21 is concluding the first 4 months and Ga7-6 is concluding the second group of 4 months. Together they define the end of the first two tertials (from winter solstice). 2 * 21 = 42 = 7 * 6.

 

We know that the first part of the henua calendar in G exhibits 7 and the second part 6. Waxing is connected with black, from the origin as seen at new moon. Waning is connected with the full white moon. Darkness is connected with 7 (as the number of 'planets'), 6 with light (sun).

42 is here defined in two different ways, first as in the ancient Egyptian judges of the dead, then as - maybe - 6 weeks. Ariki in Ga6-3 is already in the waning part of the henua calendar (in period 21). 144 = 12 * 12 and 8 * 26 says the end of early spring has been reached.

Between the featherless ariki (Ga2-21) and ariki in Ga6-3 there are 90 days, i.e. there are 4 + 3 = 7 months from winter solstice. 64 + 144 = 208 (as in 20 and 8). If we count with summer solstice as 182 days beyond winter solstice, then Ga6-3 will come 208 - 182 = 26 days later.

Next page is the last and summary page:
 

 

Ariki glyphs serve in G to demarcate distance from winter solstice, for instance:

114 123
Gb6-26 Ga2-21 (52) Ga7-6 (176)
116 = 4 * 29 124 = 4 * 31
240 = 8 * 30

'Feathers' on the head indicate that sun is 'present' (and not away far in the north with his 'winter maid').

Ariki glyphs seem to be located as last glyphs seasons (cfr above). In Ga2-21 the top left 'limb' is ending with a vertical short line and in Ga7-6 it is the right top 'limb' which is similarly 'cut off'. The sign evidently means 'a tertial is ending here'.

A variant without headgear and looking straight ahead at us probably is indicating a more important cardinal point:

259 = 7 * 37
Gb1-7 Ga1-24
261 = 9 * 29