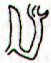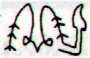Maybe once the year was considered to be formed by 4 seasons equally long and each with very many days, expressed as a 'hundred'. Reflection then concluded the year must be formed like a square. 400 = 20 * 20.

Experience taugth 400 were too many days, but the idea of a square lingered on. The familiar moon was more easily measured. The visible moon has 28 nights, and if it was imagined as a square, it measured a week on each side. But moon was two persons, waxing and waning. Each should have a fortnight.

Extending the measure twice 7 to reach the many days of the sun, it could be combined with 10 (i.e. as far as you were able to count on fingers and toes) and 140 was the natural answer.

400 was, though, a majestic not to be ruled out ancient measure for the year, and beyond 140 it necessitated an additional 260, which thereby aquired a status quite similar to 400.

But 140 was too short. Extending 140 with a month (28) resulted in 168, which was not so bad, considering that observing stars they were not possible to see all the time - when sun inhabited their stations.

168 needed to be completed to reach the full year (there was only one sun person - not two as in the moon). The remedy was searched for by the same method which gave 260. The single 360 (obvisously a number related to 260) had to be reached by adding 192 to 168.

Next pages:

The 24th - 25th periods in G refer to a cardinal time for the sun (the mouth of kiore is different in Ga6-16 and Ga6-18 compared with the normal mouth - as for instance in Ga6-11): 23 Ga6-9 Ga6-10 Ga6-11 24 Ga6-12 Ga6-13 (168) Ga6-14 Ga6-15 Ga6-16 25 Ga6-17 Ga6-18 The parallel periods in K include a peculiar arrangement with a double henua (Kb3-8), which we maybe should compare with the double 'fire fingers' in Ka3-14--15 Kb3-1 Kb3-2 Kb3-3 Kb3-4 Kb3-5 Kb3-6 Kb3-7 (144) Kb3-8 Ka3-10 Ka3-11 Ka3-12 Ka3-13 Ka3-14 (60) Ka3-15 Ka3-16 The distance from Ka3-14 to Kb3-7 is 84 days.

There ought to be some kind of message embedded in these parallel presentations: 83 Ka3-13 Ka3-14 (60) Kb3-7 (144) 100 Ga2-25 Ga2-26 (57) Ga6-17 (158) Although the structure is similar, the contents are different. The signs are quite dissimilar. My expectation that hanau glyphs should be connected with water finds support in the text of K, because there is a ua sign immediately before hanau: Kb3-1 Kb3-2 Kb3-3 Kb3-4 Kb3-5 Kb3-6 Kb3-7 (144) Kb3-8 K has only this hanau glyph to offer us, and ua in Kb3-5 is the only true ua glyph in K. 'Water' (rain, ûa) in Kb3-5 is giving birth to a little 'eye'.

144 is a square and adding another square, 36, we will reach 180. By adding the distance between Kb3-7 and Ka3-14 to 144 we will reach 228 = 8 * 28½, i.e. 36 days beyond the end of the text of K:

 

		82		35	...	11		35	-
Ka3-14 (60)	Ka3-15		Kb3-7 (144)		Kb5-8 (180)		Kb5-20		228
	84			36		12		36
				84
	168 = 6 * 28

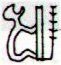
I decide to add this thought provoking table with comments:

... K has only this hanau glyph to offer us, and ua in Kb3-5 is the only true ua glyph in K. 'Water' (rain, ûa) in Kb3-5 is giving birth to a little 'eye'. What the character of this 'baby' is can be guessed at by counting.

Kb3-1 Kb3-2 Kb3-3 Kb3-4 Kb3-5 Kb3-6 Kb3-7 (144) Kb3-8 144 is a square and by adding another square, 36, we will reach 180. 144 and 36 are 'reflections' of each other in 180 (like 192 and 168 in 360). But in K there are (or rather presumably once were) 192 glyphs. Therefore we should not add 36. Instead, by adding the distance between Ka3-14 and Kb3-7 to 144 we will reach 228, i.e. 36 days beyond the end of the text of K: 82 35 ... 11 35 - Ka3-14 (60) Ka3-15 Kb3-7 (144) Kb5-8 (180) Kb5-20 228 84 36 12 36 84 168 = 6 * 28 228 = 60 + 168 = 8 * 28½ (the first measure of Te Pei in G): Ga8-24 (228) Ga8-25 Ga8-26 Gb1-1 Gb1-2 (232) Gb1-3 Gb1-4 Gb1-5 Gb1-6 (236) Gb1-7 Gb1-8 Gb1-9 The key numbers 192 (equal to 8 * 24 as in Ga8-24) and 228 will lead us to the 'land of 8' (Te Varu Kainga), which is literally unseen in K, but possible to find in G: 191 Ga2-3 (34) Ga8-24 (226) 192 = 8 * 24