A long right leg
presumably indicates there is 'much birth' ahead, while a long
left leg should mean that the season of much birth lies in the
past.
Both man and
time can run, but only time can flow. The imperceptible
flow of time around solstice cannot be illustrated by a
man running.
Next pages:
|
The distance from the first to the second of the two redmarked
hanau glyphs is 68:
 |
67 |
 |
|
Ga6-17 (158) |
Ga8-24 (226) |
8
* 24 (as in Ga8-24) = 192 (which is the number of glyphs in K).
226 - 192 = 34, the ordinal number of a moe
glyph we recognize:
|
The appearance of 192 in connection with a calendar based on 360
days makes it possible to guess why:
The 'reflection' of 192 in 360 is 168 (i.e. 192 + 168 = 260).
Both 192 and 168 are 'square' numbers: 4 * 48 = 192 and 4 * 42 =
168.
In other words, a year with 360 days can be divided into two
unequal 'years' ('quadrangular earths').
The 'squaring of the circle' can be accomplished by using two
'squares'.
Likewise, we can take a 400-day long year and 'square' it with
the described method:
We recognize both
260 and 140 from the rongorongo texts, and there are also
some signs of a 'year' with 400 days. 4 * 65 = 260 and 4 * 35 =
140. With some new respect we can now consider those places in
the texts where we have met 65 and 35, e.g.:
|
G |
period no. |
number of glyphs |
|
1, 2, 3 |
8 + 4 + 7 = 19 |
35 |
19 |
|
4, 5, 6 |
3 + 2 + 3 = 8 |
27 |
|
7, 8, 9 |
4 + 2 + 2 = 8 |
35 |
|
10, 11, 12 |
2 + 3 + 2 = 7 |
35 |
42 |
|
13, 14, 15 |
4 + 3 + 5 = 12 |
54 |
|
16, 17, 18 |
3 + 6 + 7 = 16 |
70 |
|
19, 20, 21 |
5 + 8 + 5 = 18 |
30 |
88 |
|
22, 23, 24 |
4 + 3 + 5 = 12 |
100 |
|
25, 26, 27 |
2 + 2 + 3 = 7 |
30 |
107 |
|
28, 29, 30 |
3 + 3 + 4 = 10 |
117 |
|
31, 32, 33 |
6 + 4 + 3 = 13 |
130 |
|
34, 0 |
3 + 7 = 10 |
10 |
140 |
|
192 days
appeared also at haś in Ga7-23, when we counted
from Gb8-30:
 |
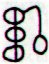 |
153 |
 |
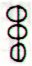 |
 |
|
Ga7-23 (192) |
Ga7-24 |
Gb4-26 |
Gb4-27 (348) |
Gb4-28 |
|
156 = 12 * 13 |
My guess of
the complementarity between 192 and 168 cannot be tested
by this example - it must of course be true:
 |
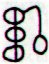 |
 |
|
Ga7-23 (192) |
Ga7-24 |
Gb5-6 (360) |
|
168 |
The other case
calls for investigations both towards left and towards
right. First at right, 226 + 168 = 394, and 394 - 230
(the glyphs on side a) = 164:
 |
191 |
 |
 |
166 |
 |
|
Ga2-3 (34) |
Ga8-24 (226) |
Ga8-25 |
Gb6-11 (394) |
|
192 = 4 * 48 |
168 = 4 * 42 |
This result is
not very convincing, but 6 * 11 = 66 looks like 166, an
important rongorongo number. Instead, let us look towards left:
 |
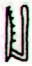 |
132 |
33 |
 |
196 |
108 |
|
Gb4-18 (339) |
Gb4-19
|
Ga2-3 (34) |
|
168 |
The
result indicates 167 rather than 168, though, because we have recently seen:
 |
149 |
 |
40 |
109 |
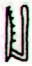 |
|
Ga2-9 (40) |
Ga7-21 (190) |
Gb4-19 (340) |
|
150 |
150 |
Here we can alternatively
read 40 + 150 = 190, followed by 40 + 110 = 150. Then we can add 150
+ 110 and get the important number 260. Maybe that is what is expected of the reader.
Still, the end comes with Gb4-19 (although the vertical measurement
is at extreme left).
Maybe we should shift two
glyphs to the left, and then voilą a much better result, with
a more normal tagata before and with the last glyph as
hipu:
 |
 |
148 |
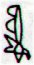 |
 |
41 |
107 |
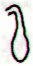 |
|
Ga2-7 (38) |
Ga2-8 (39) |
Ga7-19 (188) |
Ga7-20 (189) |
Gb4-17 (338) |
|
150 |
150 |
 |
 |
132 |
33 |
 |
196 |
108 |
|
Gb4-18 (339) |
Gb4-19
|
Ga2-3 (34) |
|
168 |
Yet, there is a
measurement of 167 counting from Gb4-19 up to and including
Ga2-3.
Luckily I have not written
anything in the glyph dictionary about a pattern stretching twice
150 days beyond Ga2-9.