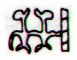After securing (as far as that has been possible with a minimum of effort) a beginning at Aa2-6, and by counting from Aa1-1 with 2 glyphs per day we have reached:

		361
Aa2-6 (96)	Aa2-7		Aa6-43 (459)	Aa6-44
182 days (?)

The question mark is motivated by uncertainty - maybe we sometimes (in Tahua) should count only 1 glyph per day? We leave that question and insert the two remaining tagata pau glyphs:

		134			194		30
Aa2-6	Aa2-7		Aa3-57	Aa3-58 (233)		Aa6-12 (428)		Aa6-43
	136 = 2 * 68			195 = 13 * 15		32

Using 459 (at Aa6-43) we can count 4 * 59 = 236 = 8 * 29.5 and similarly 428 (Aa6-12) could be read as 4 * 28 = 112 = 8 * 14. In Aa3-57 we have 2 * 32 = 64 = 8 * 8. Aa2-7 and Aa3-57 together measure out 136 glyphs, just like Ga3-7 and Ga7-33. The distance from 97 to 233 is equal to that from 67 to 203:

	135		162
Ga3-7 (67)		Ga7-33 (203)		Gb5-12 (366)
136 = 100 + 6 * 6		164 = 100 + 8 * 8
300 = 10 * 30

364 (in A) emerges as 332 + 32, where 332 can be read as 3 times 32, and we could count 4 * 32 = 128 = twice 64 (= 8 * 16). There are 2 cycles in a year, each like a square measuring 8 by 8.

Another way of drawing the map is to start with 270 = 9 months à 30 days, and then divide in the middle to reach 135:

		134			194		30
Aa2-6	Aa2-7		Aa3-57	Aa3-58 (233)		Aa6-12 (428)		Aa6-43
		135 = 9 * 15		195 = 13 * 15		32

22 * 15 = 330 is equal to 11 months. After adding 32 and Aa2-6--7 we have 364.

There are two pau (hipu) signs in Aa6-43. The double sign implies it is the 2nd cycle which is reaching to its end, and 459 / 2 = 229.5 suggests Te Pei could be the station at the end of the 2nd cycle. The 1st cycle of the year would then begin not at winter solstice but at summer solstice.