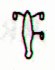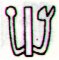next page

previous page

up

home

We have 14 glyphs at the beginning of side a in Tahua before reaching the extracalendrical night Aa1-15:

These 14 glyphs could represent 26 nights each: 14 * 26 = 364. But the last updated version of the structure does not quite fit with this pattern. We counted 13 * 28 = 364 nights, not 14 * 26 = 364 nights. From the assumption that the fundamental unit was a month with 28 nights we reached the conclusion that there must be 13 months in a year. Changing the assumption to a fundamental unit with 14 nights, there must be 26 periods in a year.

That means we should change the structure into:

No longer can we see a connection between number of glyphs and number of fundamental periods. We have to assume that each glyph stands for 2 periods (= 28 nights). The 10 solar months we had guessed at (Aa1-1 -- 10) will have 20 fortnights, a nice number.

The moon will have 84 nights = 6 fortnights, also a nice number, suggesting a relationship with the sun. But if we assume each moon-time glyph to have 2 fortnights, then the number of moon-time glyphs must be 84 / 28 = 3 glyphs. Are they Aa1-13 -- 15 (the earlier suggested X-area)? No, that would leave Aa1-11 -- 12 without 'ruler'.

Are they Aa1-11 -- 13? That would leave Aa1-14 without explanation.

Unless, of course, we say that Aa1-14 (marai according to Metoro):

is the extracalendrical time glyph (= 365 - 364), and regard Aa1-15

as the fraction between the true length of a year and 365, which sounds reasonable, as we already earlier had arrived at that conclusion:

'The explanation of Barthel about 'sitting like a tailor' (Schneidersitz) meaning 'submission' and 'slavery' cannot be true; the newborn year has open leg ends too, perhaps with a message similar to the sign of the unclosed arm.

Though I prefer another explanation - at least provisionally - viz. that the 'unfinished' members amount to fractions, they are less than 1. The year is longer than 365 days and we get a more exact measure if we add 1 night every 4th year. The little chicken at right above has only one whole member, the right wing. Only 1 of the 4 possible members are drawn complete: He is just ¼ of a full day.'

One argument against the new solution is that the glyph Pa5-67, which is parallel to Aa1-13, does not arrive until far later than the glyphs in P which are parallel to Aa1-1 -- 12. But we have to leave this argument until later, we cannot answer all question at once

The week is divided in two, that we saw also in Ab6-42--57 (16 glyphs):

From the week (7 nights), multiplying with 2, we reach a fortnight (14 nights) and then the pattern may continue forever (7, 14, 28, 56 ...).

However, the glyphs Aa1-1 -- 12 do suggest that we should not go further than 56:

Let us now have a look at the new version of the structure at the beginning of side a in Tahua: