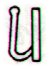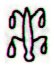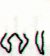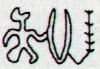|
TRANSLATIONS
Strangely we returned to pito. But I think it is a bit premature, we should continue with the 7 + 6 + 7 structure in H a bit longer. Because we have seen this structure stretching from Hb7-7 to Hb8-105 and we should complete the last of the discovered 26-groups:
Will the 26-group pattern continue? And can we use the pattern 7 + 6 + 7 + 6 = 26 in order to restore how many the lost glyphs presumably were? For the moment I have this description documented (under Large Santiago Tablet / O(bject) / Next page:
In this table I have marked with red lines where there is uncertainty. Though by using the formulat 314 + 20 + 314 we have already learnt that line a6 ought to be changed from 69? into 70 (?). I have not changed in the table above yet because a just mechanically made change would increase 648? into 649 (≠ 314 + 20 + 314). Somewhere in the lines on side a beyond a6 an adjustment probably is needed. They did not use punctuation marks in the rongorongo texts. Perhaps we have found out why they were not needed, it is easy to count to 6 or 7 without really counting - a glance is sufficient. Said and done. We continue beyond Hb8-105 and find what presumably is a 7-group:
But beyond Hb8-112 I doubt there is a 6-group, the visual clues in the glyphs do not suggest that. If I am right, then we have to complete the table above into:
At Hb9-17 the calendar of the week is beginning. The interval from Hb8-113 to Hb9-17 is 43 glyphs and 43 - 6 = 37 is a number which is not divisible by 13. Neither is 43 divisible by 13. Instead I suggest what follows is a group with 16 glyphs according to the pattern 5 + 6 + 5:
Maybe we therefore should extend our pito group into:
That leaves us with 43 - 16 = 27 glyphs remaining until we reach the weekly calendar. In the sequence with 27 glyphs we have an external parallel:
The 9 glyphs in H obviously is a unit. 27 - 9 = 18. From Hb9-4 and up to the weekly calendar we have the 9-glyph group + a group with just 4 glyphs (9 + 4 = 13):
The symmetrically designed Hb9-14--15 suggests that we are reading the structure correctly. Before the 9-group it looks as if we may have two 7-groups (7 + 7 = 14):
In short:
The calendar of the week can be described as 16 + 6 + 20 = 42:
After this calendar we have from Hb9-59 up to the end of the text at Hb12-49 a number of glyphs (177?) which is not divisible by 13:
One of the experiences gained so far is that we cannot trust 7 + 6 + 7 + 6 = 26 to be a pattern everywhere. The pattern may for instance be 7 + 6 + 7 = 20, or there may be a sum which is 36 (= 7 + 6 + 7 +16) or 42 (= 16 + 6 + 20). Or the sum may be 27 (= 7 + 7 + 9 + 4). The 177? remaining glyphs at the end of the H text should be divided into two parts, because the parallel text in P ends like this:
The question mark after 50 for the glyphs in line b12 is due to the fact that there seems to be a glyph missing at the very end of the text:
A parallel in B suggests that too:
But could there perhaps be 2 glyphs missing? It would result in more beautiful numbers. The sum should not be an odd number:
104 is a 'cosmic number', it is equal to 4 * 26 = 8 *13. Could the creator have missed that opportunity? I doubt it. The conclusion is that we ought to reduce 55? into 54?
Why is there an imbalance (344 / 304 respectively 308 / 340)? Maybe the creator tried to add pairwise: 344 + 308 = 652 = 4 * 163 304 + 340 = 644 = 14 * 46 304 + 308 = 612 = 17 * 36 = 6 * 102 340 + 344 = 684 = 4 * 171 = 6 * 114 = 19 * 36 19 * 36 certainly is interesting. Maybe 612 (with a question mark) should be corrected into 608 = 19 * 32 and the sum of the glyphs be 19 * (36 + 32) = 1292? The Tahua text is based (among other things) on the equation 29 * (16 + 26) = 1218. But 648 = 8 * 81 = 9 * 72 = 18 * 36 is much better than 19 * 36. Furthermore, we had another formula in mind: 2 * (314 + 20 + 314) = 1296 = 16 * 81 = 4 * 4 * 9 * 9. If we rearrange the table above to visualize where we have found the two 20-groups, it becomes:
44 (?) + 20 + 6 in line a6 has the sum 70 (?) according to results we have arrived at. But the 'ugly' sum 319 cannot be correct, I think. If we reduce 319 to 318 it becomes much better. The way to do this is once again to correct the number of missing glyphs between Ha6-19 and Ha6-101, this time from 6? back to the earlier 5?:
The number of glyphs from Ha1-1 up to and including Ha6-101 will then be 300 (not 301 as we thought a while ago):
The reconstructed glyph number for Ha6-101 will be *Ha6-24 (instead of *Ha6-25), with corrections caused by subtracting 1 in all the following reconstructed glyph numbers:
The 20-group will have these reconstructed glyph numbers and ordinal numbers:
After this cumbersome operation I once again give a table with updated results:
With red I have now indicated the remarkable fact that we have a pattern 20 + 6 = 26 on side a as the final of the first 6 lines, while on side b the mirror pattern is 6 + 20 = 26 as the start of the second group of 6 lines. We advance in knowledge, albeit slowly. Investigating the details of the new pattern: 318 + (20 + 6) = 344 glyphs in the 1st half on side a 310 - 6 = 304 in the 2nd half on side a 314 - 6 = 308 in the 1st half on side b 314 + (6 + 20) = 340 glyphs in the 2nd half on side b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||