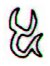TRANSLATIONS

TRANSLATIONS

Next page (the last one from the hyperlink 'conclusions'):

Although Tahua is a long and difficult text it is fairly evident that the presented internal parallel glyph sequences describe similar events in winter respectively summer:

winter
winter	Ab7-33	Ab7-34	Ab7-35	Ab7-36	Ab7-37	Ab7-38	Ab7-39
summer				-		-
summer	Aa5-14	Aa5-15	Aa5-16	-	Aa5-17	-	Aa5-18

The backs of Ab7-34 and Aa5-15 resemble that in Eb8-26, and we have parallels in henua glyphs at the beginning of the sequences together with hakaturou variants at the end:


Eb8-20	Eb8-21	Eb8-22	Eb8-23	Eb8-24	Eb8-25	Eb8-26

Henua glyphs mark the end of calendrical cycles, therefore we presumably should read about winter solstice (Eb8-20--26 and Ab7-33--39) respectively summer solstice (Aa5-14--15).

Ab7-36 probably represents the old and new years - which of course cannot occur at summer solstice, where only the old half-year meets the new half-year.

Maybe the little 'bulb' at bottom in the summer henua ora is illustrating earth? Sun (and presumably also the sky) stands high at summer solstice. At winter solstice earth and sky are closer (Ab7-33).

We have established a probable connection between the standard tara glyph (with a prominent tail) and winter solstice. In Tahua there are two glyphs of this kind, Ab7-37 and Ab8-69, the first of which is among the winter solstice glyphs:


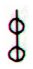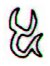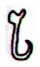Ab7-33	Ab7-34	Ab7-35	Ab7-36	Ab7-37	Ab7-38	Ab7-39

Ab8-69 is located even further towards the end of side b (which occurs at Ab8-84), having a position 26 glyphs ahead of the 'navel' (pito):

		25		14
Ab8-42	Ab8-43		Ab8-69		Ab8-84
42 = 26 + 16	26		16

Ab8-69 is drawn identical with Ab7-37, i.e. the meaning must be identical too.

The 'navel of the island' (te pito o te henua, 'centre of the world') must be on the western coast. The 29th kuhane station (alluding to the 29th black night of the moon) she named 'Te Pito O Te Kainga A Hau Maka O Hiva' (possibly indicating that the entire island lay in darkness and that therefore no further geographical location could be pinpointed).

From the hyperlink 'the meaning must be identical too' we reach this page:

Among the 42 glyphs (maybe 3 weeks) from pito to the end of the line I have redmarked a few of the significant ones:


Ab8-43	Ab8-44	Ab8-45	Ab8-46	Ab8-47	Ab8-48

Ab8-49	Ab8-50	Ab8-51	Ab8-52	Ab8-53	Ab8-54

Ab8-55	Ab8-56	Ab8-57	Ab8-58	Ab8-59	Ab8-60

Ab8-61	Ab8-62	Ab8-63	Ab8-64	Ab8-65	Ab8-66

Ab8-67	Ab8-68	Ab8-69	Ab8-70	Ab8-71	Ab8-72

Ab8-73	Ab8-74	Ab8-75	Ab8-76	Ab8-77	Ab8-78

Ab8-79	Ab8-80	Ab8-81	Ab8-82	Ab8-83	Ab8-84

Ab8-52 (with an ordinal number to draw our attention) is a variant of henua ora (i.e. marks the end of a cycle).

Ab8-60 and Ab8-76 (16 glyphs ahead of number 60) are henua bent the normal way, reminding us about the 'shell of Tagaroa' (and in Ab8-63 we have pure).

Ab8-64 and Ab8-83 (19 glyphs ahead of number 64) exhibit an unusual variant of henua with obliquely cut off bottom end. In the K text there is only one such glyph, viz. at the very end of the last (29th) period:

29
29	Kb4-10	Kb4-11	Kb4-12	Kb4-13	Kb4-14

Neither has Tahua any more glyphs of this kind. The creators of the Tahua and the London Tablet texts are using the same 'vocabulary'.

Henua cut off at the top probably means that the 1st half-year has come to a stop. This takes place at the end of the 14th period according to K:

13
13	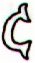Ka5-13	Ka5-14	Kb1-1
14
14	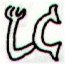Kb1-2	Kb1-3
15
15	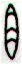Kb1-4	Kb1-5	Kb1-6

In Tahua there is also one glyph of this type:


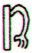Aa4-31	Aa4-32	Aa4-33	Aa4-34	Aa4-35
ki te tagata amo hia	i te henua	ko te tagata kua ui	i tona henua	kua moe ia kua huru ia

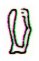
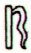Aa4-36	Aa4-37	Aa4-38	Aa4-39	Aa4-40
i tona henua - kua oho te vae - ku totohu - i tona henua - e mai tae kake hia - ki te henua - ki uta ki te pito o te henua				ko te henua - ma to rima

At Aa4-39 is 'ki uta ki te pito o te henua' (the high up navel of the land), which agrees with Aa4-34 denoting the end of the 1st half year. The 1st half year begins at winter solstice and ends at summer solstice.

There ought to be a numerical 'proof' in the glyph distances between Ab8-64 and Aa4-34:

a1	90		285	b1	82		644
a2	85			b2	85
a3	76			b3	77
a4	34	82		b4	80
	48		385
a5	83			b5	80
a6	84			b6	92
a7	85			b7	84
a8	85			b8	64	84
					20		20
sum	670			sum	664

20 + 285 = 305 = 5 * 61. Counting long (which possibly should be more correct) gives 306 = 17 * 18. Counting short we have 304 = 16 * 19.

The other distance is 385 + 644 = 1029 (maybe to be read as 10 and 29 - numbers at which sun respectively moon not are visible). 1029 = 3 * 7 * 7 * 7 = 21 * 49. Counting long we get 1030 (maybe meaning 10 and 30).

The possibilities are many. Possibly we should calculate the ratio between the shorter and the longer distances:

305 / 1029 = 0.2964 and 304 / 1030 = 0.2951

Counting the long distance long and the short distance short we reach numbers we recognize:

... The 1st viri is already counted (long together with the 4th viri). Therefore there is only one possible counting mode left, viz. short. The result is 16 and we immediately think of Aa4-72. Let us now count the distances (forwards and backwards) between te pito and Aa4-72:


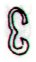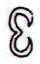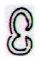short →	long →	short →	long →	short →	long →
16	44	520	466	16	272
*20 29**			*26 29**
1334

The counting modes become beutifully arranged. The normal counting modes have disappeared and there are regular undulations between short and long. The distances between te pito and Aa4-72 are 44 + 520 + 466 = 1030 respectively 16 + 272 + 16 = 304.

Neither number is a multiple of 29. Maybe we should read them as 10-30 respectively as 30-4? Another idea is to divide 304 by 1030. The result is 29.51 % and one comes to think of the possibility of this measure having been created to describe the lunar month, not 29, not 29 ½, but a more precise measure. According to Wikipedia, the synodic month is 29.53 days. How close can you get to that number by the method imagined (division of two numbers less than 1,334)? If we increase from 304 to 306 (we must use only even numbers), 1030 will shrink to 1028 and then we get 29.77 % ...

If now in Tahua the glyph distances between henua cut off at the top and henua cut off at the bottom once again repeats numbers creating the cycle of the visible moon, that hardly is a coincidence. Either my imagination is remarkable or there is a moon cycle message embedded in the Tahua text.

In the latter case we here have an explanation why it is so difficult to find equally long glyph distances for summer and winter.

As to the text in K a similar explanation should be searched for:

a1	24		97	b1	3	22	3
					19		67
a2	10	22		b2	14
	12				4
a3	14			b3	16
	7
a4	14	16		b4	14
	2				5		25
a5	14			b5	20
sum	97			sum	95

The longer distance measures 25 + 97 + 3 = 125 (counted normally) and the shorter 67. 125 = 5 * 5 * 5.

The ratio is 67 / 125 = 0.536 which cannot allude to the cycle of the moon.

Counting the long distance long and the shorter short gives 66 / 126 = 0.52 which possibly indicates the 52 weeks in a year.