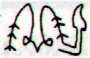TRANSLATIONS

next page previous page up home

Next pages:

Instead of looking back in time from Ga4-2 we should look forward, because a new season forces itself upon an old one. The young and powerful pushes the old and weak away. The time of change is determined by the new season, not by the old. If Ga4-2 is the last sign of the takaure season, then Ga4-3 must be the first glyph of next season, and we can call it 'summer':
summer 148 128
Ga4-3 Gb1-6 Gb5-11 Gb5-12
86 235 364 1
1 150 279

Counting from the first glyph of the text haga te pau (Gb5-12) will be glyph number 365. Counted from Ga4-3 it is number 280, a number which suggests 10 months with 28 nights in each.

However, the calendar is much more intricate than this, which will be proven here.
We have two firm points to stand on, the beginning of summer at Ga4-3 and the central point at Gb1-6:
summer 148 128
Ga4-3 Gb1-6 Gb5-11 Gb5-12
86 235 364 1
1 150 279

150 is a number which suggests there are 5 months with 30 days in each from Ga4-3 up to and including Gb1-6.

On the other hand 279 = 9 * 31, seemingly to tell us that a month has 31 days (not 30). This paradox will now be explained.
Assuming there are 31 days (= glyphs) in every month of summer, we must arrive at Gb1-11 after 5 months, not at Gb1-6:
Gb1-4 Gb1-6 Gb1-7 Gb1-8
149 150 151 152
Gb1-9 Gb1-10 Gb1-11 Gb1-12
153 154 155 156

The flanking birds in Gb1-4 and Gb1-12 makes a symmetrical pattern together with Gb1-6 and the 155th glyph Gb1-11. These birds are marks to make us focus our attention.
Assuming next that instead there are 30 days (= glyphs) in every month of summer, we must arrive at Gb5-2 after 9 months, not at Gb5-11:
Gb4-33 Gb5-1 Gb5-2 Gb5-3 Gb5-4 Gb5-5 Gb5-6
268 269 270 271 272 273 274
Gb5-7 Gb5-8 Gb5-9 Gb5-10 Gb5-11 Gb5-12
275 276 277 278 279 280

9 * 30 = 270 measures 9 months of the 360 days in a regular year, while 279 would measure 9 months of a year with 372 days (which obviously is wrong).

The reversal illustrated with Gb4-33 and Gb5-1 marks an important calendar point, and we have earlier noted how it is located at the beginning of the 4th quarter of the text:

2nd half year 116 10 106
Gb1-7 Gb4-33 Gb5-1 Gb5-12
236 353 354 365
3rd quarter of text 4th quarter of text

With Gb5-12 (haga te pau) as the 365th and last glyph (day) of the year it seems to indicate how the year is ending after 9 months, viz. after 9 months of summer. 471 * 75 % = 353.25.

Having read so far, thoughts tumble around. How can there be 471 glyphs = days? What happens beyond haga te pau? There are 2 * 53 glyphs beyond Gb5-12. And 7 * 53 = 371. Maybe there is a year which ends at 371 + 1 = 372 = 472 - 100?

Increasing from 471 to 472, which is the true length of the text, 75 % will mean 354 = 29.5 * 12. Let's move on:

The two alternatives (30 respectively 31 days per month in summer) give these results:
30 days 148 119
Ga4-3 Gb1-6 Gb5-2
1 150 270
31 days 153 123
Ga4-3 Gb1-11 Gb5-11
1 155 279

But - to repeat - 279 would measure 9 months of a year with 372 days, which hardly is right. On the other hand will 270 days not stretch all the way to haga te pau, which also is strange. The correct reading of the text instead is a third alternative:

summer 148 123
Ga4-3 Gb1-6 Gb5-6
1 150 274

There are 5 months with 30 days to Gb1-6, and then follows 4 months with 31 days. Part of the proof of this being the correct reading is the fact of finding a tagata glyph (fully grown) at the end.
If we look at the ordinal numbers counted from the beginning of the text we suddenly will understand what is meant:
Gb4-33 Gb5-1 Gb5-2 Gb5-3 Gb5-4 Gb5-5 Gb5-6
354 355 356 357 358 359 360
Gb5-7 Gb5-8 Gb5-9 Gb5-10 Gb5-11 Gb5-12
361 362 363 364 365 366

There are three different and equally true alternatives. Tagata at Gb5-6 stands at the end of a regular 360-day solar year, Gb4-33 is the last glyph in a year measured by lunar 29.5 nights per month (354 = 12 * 29.5), and Gb5-11 is number 365 (our own kind of year).

A fourth way of counting the year is as 364 = 13 * 28, visualized with vaha kai (a mouth ready to eat) in Gb5-10.

Haga Te Pau now appears in a new light: It is the difference between the true year length 365¼ and 365. The pau foot illustrates one of the four limbs as if a little sun was hidden inside.

Finally, to reach the correct numbers (e.g. 360 at tagata) it is necessary to count from the last glyph (Gb8-30) on side b:

Gb8-30

229 (side a) + 242 (side b) = 471 glyphs should be imagined as 230 + 242 = 472, because Gb8-30 should be counted twice. 472 = 2 * 236 = 4 * 118 = 8 * 59 = 16 * 29.5.

Q.E.D.

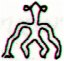
The Excursion is then completed with a final page:

We have arrived at the conclusion that Ga4-2, a glyph probably depicting a flying insect (takaśre), is located as the end point of the season which (according to the G text) precedes summer. Together with the preceding tagata (a fully grown season) Ga4-2 may have been referred to as 'haga takaśre':
5 * 30 150 summer
4 * 31 124
Ga4-1 Ga4-2
'haga takaśre'
summer: 148 123
Ga4-3 Gb1-6 Gb5-6

The task is completed. It did not encompass any explanation of why the kuhane station Hanga Takaure is located so close to Poike. The answer to that question must wait until later.

A final note: The neck in Gb5-6 is markedly longer than the neck in Ga4-1. On the other hand is Ga4-1 drawn as a greater figure. These differences are certainly meant to be understood by the reader.