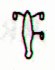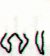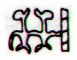TRANSLATIONS

TRANSLATIONS

In the glyph dictionary we have arrived at GD21, hua poporo. The only glyph in Tahua belonging to the type hua poporo is Aa1-14:

			-	-
Aa1-13	Aa1-14				Aa1-15
kua tuu	marai				i tona ohoga - ki te ariki
...	...	...
			Ha6-101	Ha6-102	Ha6-103	Ha6-104	Ha6-105

Pa5-67	Pa5-68		Pa5-69	Pa5-70	Pa5-71	Pa5-72
This sequence of glyphs does not appear in Q

I guess there is a relationship between hua poporo and hura (GD88), perhaps resembling what we found in the Mamari moon calendar, where similar, though 'mirrored', glyph types indicate reversal:

3			'branch' not broken, but the 'fruit' is heavy
	Ca7-15	Ca7-16
4	'branch' 'breaks'
		Ca7-23	Ca7-24

If such a relationship exists, then we note the sound similarity between hua and hura. If one of these words allude to the moon and the other to the sun, we surely must relate hua to moon and infer that sun is related to hura. In the next step we can combine glyph types with words using Metoro's translations:


hua poporo	*hura*
moon	sun

If my guess is correct, then Aa1-14 ought to be related to Aa6-55, at which point a reversal occurs:

... The turnover between variant 2 and 3 (of GD45) must be located between Aa6-41 and Aa7-19 and sure enough we there find the unique Aa6-55:


)	Aa6-55	(
Aa6-41	Aa6-55	Aa7-19

Aa6-55 is a compound between GD45 and GD88, that we can conclude from the parallel passage in Ra3-101 -- 106:


Aa6-53	Aa6-54	Aa6-55		Aa6-56	Aa6-57	Aa6-58
				-
Ra3-101	Ra3-102	Ra3-103	Ra3-104	-	Ra3-105	Ra3-106

What are the glyph distances (forwards and backwards) between Aa1-14 and Aa6-56?

Aa1-14	90-14 = 76
a2	85
a3	76
a4	82
a5	83
Aa6-56	56
sum	458
long count	459
short count	457
458 = 2 * 229	1334 - 458 = 876 = 2 * 2 * 3 * 73
459 = 17 * 27 = 3 * 3 * *3 17**	1334 - 459 = 875 = *25 35 = 5** * 5 * 5 * 7
457 = prime number	1334 - 457 = 877 = prime number

A numerical relationship probably exists.

The long count goes from Aa1-14 to Aa6-55, i.e. the shorter distance, while the opposite short count (from Aa6-55 to Aa1-14) goes the longer distance. It is - at first glance - the same pattern as we found counting viri distances:

				long count 18
Aa8-26	Ab1-1	Ab7-26	Aa4-72	long count 18	Aa5-7
normal →	short →	normal →			long →
*60 = 3 20**	*520 = 26 20**	*482 = 29 16 + 18**			*272 = 29 10 - 18**
*580 = 29 20**		*754 = 29 26**
1334

The normal count from Aa8-26 to Ab1-1 (3 * 20) includes Ab1-1. When the counting goes on from Ab1-1 to Ab7-26 it is a short count, i.e. neither Ab1-1 nor Ab7-26 is included. That means 29 * 20 = 580 is a short count measurement (neither Aa8-26 nor Ab7-26 is included).

Counting normal from Ab7-26, therefore, must include Ab7-26 but exclude the end glyph. If the end glyph is Aa5-7, at which glyph a long count starts, the measure from Ab7-26 to Aa5-7 must be normal.

580 is a short count measure, because it excludes both Aa8-26 and Ab1-1, while 754 must be its opposite - a long count measure. The conclusion is that counting viri by using Aa8-26 and Aa5-7 should be done with long count for the longer distance and short count for the shorter distance.

We have, furthermore, counted long, short and normal also at vero glyphs, finding 29 appearing there too:


Aa2-4	Aa6-29	Aa6-51	Aa8-27	Aa8-78
*→ short count: 435 (= 15 29)**		*→ normal count: 145 (= 5 29)**		51 + 27 = 78
*← long count: 899 (= 31 29)**		*← normal count: 1189 (= 41 29)**

The components (15, 31) respectively (5, 41) we can interpret as a pattern:

31	41	10
15	5	-10
16	36	20
16 and 36 their difference 20 are differences.

We can compare with a similar type of pattern for hua poporo and hura:

		differences
Aa1-14	Aa6-55	differences
long count *→ 459 = 17 27**	short count *→ 875 = 25 35**	*416 = 8 52**
27	35	8
17	25	8
10	10	0

In summary, 1334 equals 17 * 27 + 25 * 35, and also 8 * 52 + 918 (= 2 * 459).