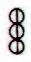|
TRANSLATIONS
The triplet of
rhombs, as for instance in Aa1-78 and Aa1-84:


maybe means
those 3 quarters when sun is present. If so, then they may stand
for 3 * 91 = 273 days.
Metoro's
standard inoino at this type of glyph ('Ce qui est
éclarante, rayonnant' according to Jaussen.)
could then be explained as 'what is bathing in the rays from the
sun'.
We must
consider once again some of the earlier thoughts as condensed in
the glyph dictionary:
|
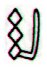
Ab6-88:

Here the 'balls' are changed into
rhombs, meaning three lunar double-months. Wheareas
the solar double-months have 2 * 30 = 60 days, the
lunar double-months have 30 + 29 = 59 nights.
There is no vertical straight line
in the middle of the glyph. 59 is an odd number and
cannot be divided into twins. Also there is no
measurement, the moon is a 'clock' in itself.
The four
corners in the rhomb marks where periods of 14
nights are completed. 4 * 14 = 56 = the number of
nights in a two-month period when the moon is
visible.
In a
rhomb the 14 nights when the moon is waxing may be
seen as the upwards going line at left, the apex
being the time of full moon. The waning moon will
then be represented by the downwards sloping line at
right. At the time of new moon we turn the rhomb 180º
similar to when we start to read a rongorongo
tablet (though here clockwise instead of
counter-clockwise), and after that we can start once
again with the waxing moon of the new month.
Moon and
sun are complementary. And the texts on the
rongorongo tablets turn counter-clockwise only
every odd turn, the even turns are clockwise. Right
and left alternate, just like sun and moon. The sun
is right, the moon is left.
The
counter-clockwise movement seems to be connected
with the sun (south of the equator) and the
clockwise movement therefore with the moon.
Consequently, the waning moon should be the
downwards sloping line at right.
"The
'second list of place names' appears for the first
time in Ms. E. The sequence of the places named runs
opposite to Hau Maka's 'first list of place
names'. Commencing on land at a point 'that can send
signals' out to sea, the path turns to the right
along the coastline so that the ocean is always on
the left.
On the
other hand, proceeding from the land of origin with
the description of the route to the new land, Hau
Maka's place names are intended to provide a
route that starts from the ocean and along which the
ocean is always to the right.
We seem
to be dealing here with two possible inversions;
turning 'toward the sea' vs. turning 'toward the
land', while maintaining the same general direction,
which is described by the common Polynesian contrast
pair tai vs. uta, or turning 'toward
the right' vs. turning 'toward the left', facing in
the same direction at the start." (Barthel 2)
The
'first list of place names' (sun) seems to have been
handed down in writing, the 'second list of place
names' (moon) presumably was passed on with
kaikai:
"While
the 'first list of place names' is supposed to have
been handed down explicitly in writing (ta ki
runga ki te kaka), the 'second list of place
names' was passed on with the aid of a mnemonic
device in the form of recitations (patautau)
accompanied by the string-figures (kaikai)."
(Barthel 2)
Addendum:
Let us reason the
other way around: 84 divided by 3
equals 28 (the number of nights in a
month when moon is visible). 14 is
twice the weekly number, and 28 = 2
* 14. A rhomb may therefore be
understood as the period when moon
is shining on the earth. Each side
of the rhomb marks a week (not a
fortnight which I earlier
suggested).
Metoro's
reaction to this type of glyph (inoino,
bad-bad) maybe was because after 84
nights there was needed 6 nights
intercalated to reach the sun
triple-month period 90 days, a
period corresponding to the time for
moving from one of the 4 cardinal
points (solstices and equinoxes) to
the next. Still the standard
GD53 with ovals may continue to mean
6 solar months:
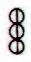
However, another
solution is to see 3 solar months
and an additional day (the vertical
straight line) to reach 91 days.
Instead of reading 3 solar
double-months we may read 3 single
solar months + 1 additional day. We
now reach a kind of symmetry between
the two glyph types:

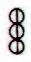
They both mean a
quarter, but the triplet of rhombs
measures 3 * 28 = 84 days, whereas
the triplet of balls measures 3 * 30
+ 1 = 91 days. The difference is a
week (7 days). We may then imagine a
greater rhomb measuring the whole
year (364 days). At each corner of
this rhomb we have an extra week,
while each side of the rhomb
measures 84 days. 4 * (84 + 7) = 364
|
|
The solar year, on
the other hand, is divided in two
halves, with 2 * 91 = 182 days in
each half. Such a half could be
represented by a double GD53, as
e.g. in Aa7-9--10:
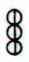 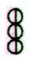
Maybe the same
sign was used to indicate the
Pleiades. One half of the year they
are 'above' and the other half of
the year they are 'below'. I think
this reading of the glyphs is better
than what I suggested earlier. |
|
4 quarters à 91
days equals 364 days for a year, followed by a 'leap' day. That
seems to be a good point from which to start the reasoning.
3 quarters are
enlightened by the sun, 1 quarter is not. Also that seems to be
a reasonable assumption.
The origin of the current line of investigation was Ab7-1:
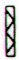
... Maybe Ab7-1 depicts the year.
3 + 1 would then, probably, mean 3 regular
quarters + 1 odd quarter (when sun is absent).
In the beginning and at the end of the year sun
is absent. 3 regular quarters could be the 3
'wives' of the sun.
Given that the year has 364 nights, a quarter
has 91 nights. 2 quarters makes 182 nights or
half a year. A rhomb could then stand for such a
half-year.
But
we mostly find 3 rhombs in a vertical row, which
then would mean 3 half-years, i.e. 3 * 182 = 546
nights. What is the meaning of that? I have a
faint recollection that the Chinese counted with
1½ year periods.
3 wives of the sun maybe explains why we find a
triplet of half-years?
182 = 13 * 14, i.e. 546 = 13 * 42. Is this fact
the reason why we find 42 so often?
546 = 6 * 7 *
13. 26 = 6 + 7 + 13. The possibilities are many
...
|
Though there are no
hatchmarks incised on the two end half-triangles.
A rhomb may
stand for a period when the sun is showering the earth with his
light rays. Therefore a rhomb may mean 28 nights and the triple
rhomb constellation 84 nights.
Alternatively, a
rhomb may mean 3 * 28 = 84 nights, i.e. the triple rhombs would
equal 3 * 84 = 252 nights. 252 = 14 * 18 and 84 = 14 * 6.
A third
possibility is that a rhomb means 56 nights (because that is the
number of nights during a lunar double month when sun 'sees' the
moon). The triplet of rhombs then becomes 3 * 56 = 168 = 14 *
12.
I think the
basic idea of a correspondence in structure between the triple
rhombs and the triple balls should be assumed.
The Pleiades (tau
ono) probably are illustrated in the rongorongo
texts by a double set of triple balls. The Belt of Orion (tau
toru) therefore may be represented by a
single set of triple balls.
The time when
the Pleiades are absent may be the origin of the idea that sun is absent
during a part of the year.
|
... In
Nilsson's book I found many strange pieces of
information, e.g.: 'Among the Nahyssan of S.
Carolina time was measured and a rude chronology
arranged by means of strings of leather with knots
of various colour, like the Peruvian quipos.
The Dakota use a circle as the symbol of time, a
smaller one for a year and a larger one for a longer
period: the circles are arranged in rows, thus: OOO
or O-O-O. The Pima of Arizona make use of a tally.
The year-mark is a deep notch across the stick...'
About
the Ibo-speaking tribes' in Africa: ...they seem to
be singularly incurious about heavenly bodies and
occurrences; however names were got for the
following constellations: - The Pleiades ('Hen and
Chicken'), the belt of Orion ('Three and Three')...
But Tautoru is the belt of Orion. 'Three and
Three' is more like the Pleiades, Tauono. I
guess that first was the belt of Orion named
Tautoru and after that the Pleiades were named
Tauono. Even the three great pyramids in
Gizeh were connected with the belt of Orion, as
shown by their locations in relation to each other
on the ground.
The
concept of two 'years', summer and winter, could
then result in the belt of Orion being seen as a
mark between those two 'years'. Moving then to the
idea of three double months in each such 'year',
they could identify the belt of Orion with a 'year'.
And as the last step in this logic the Pleiades -
about two thousand years later when the equinoxes
had moved away from Orion - would have taken over
the role of mark between the two half-years of three
double-months ... |
|
... 3
months from rise 'soon after sunset on November 20'
the Pleiades are at the meridian 'at sunset' and
then 'towards the end of April' - after another 2
months - they 'set in the rays of the setting Sun'.
The movement of the Pleiades from the meridian to
the west horizon takes an equal amount of time, I
think, i.e. ¼ of the complete 12-month-cycle. But
sun makes affirming observations impossible.
Anyhow, from 'the end of April' (when they disappear
from view as if being burned to ashes by the Sun)
until November 20 (ca 7 months) the Pleiades cannot
be seen anywhere in the night sky (if the
observation is done just after sundown) . If there
were no sun disturbing the view, there would be ca 6
months visibility and ca 6 months invisibility. Sun
destroys ca 1 month of the 'nika' period ...
... If
both early evening and late night were used for the
observations, the Pleiades could be seen in ca 11
months. During the 12th month (of invisibility) the
Pleiades perhaps went through 'recycling' (death and
rebirth). But 'nika' probably was defined as
the time of visibility given a certain observation
point (just after sunset or just before sunup)
...
...
If we think of Tauono (the Pleiades) as
having 'six stones' (tau-ono) and associate
each stone with a 'season' corresponding to one
month, then 6 could be understood as those 6 months
when they in principle would be 'above' (in the
night sky).
If
we think of the Pleiades as having 7 'stars', that
could instead mean those 7 'months' when it is not
practically possible to see them. Perhaps 7
indicates 'Moon' (nighttime) because the little
'suns' in the Pleiades do not shine during 7
'months'? Maybe those 7 'months' are refleced in
Aa7-14 etc:
|

|
|

|
|

|
|

|
|
Aa7-14 |
Aa7-20 |
Aa7-28 |
Aa7-42 |
Aa7-53 |
Aa7-63 |
Aa7-70 |
|
The Pleiades (or
the Belt of Orion) should be watched for during the early or
late night. The balls are probably to be read as tau
('stones'), while the rhombs are to be understood as the
'square' earth bathing in the light from the sun, a daytime
experience.
|
Ta'u, tau(tau)
Year (ta'u), he-hoa ite
ta'u, to confess to a crime committed long ago,
by publishing it in the form of a kohau motu mo
rogorogo (rongorongo tablet). Vanaga.
1.To hang (tau), to perch
(said of chickens on tree branches at night); rock
on the coast, taller than others so that something
can be deposited on it without fear of seeing washed
it away by the waves; hakarere i ruga i te tau,
to place something on such a rock; tau
kupega, rope from which is hung the oval net
used in ature fishing. 2. Pretty, lovely;
ka-tau! how pretty! Vanaga.
1. Year, season, epoch, age. 2.
Fit, worthy, deserving, opportune; tae tau,
impolite, ill-bred, unseemly; pei ra tau,
system. 3. To perch. 4. To hang; hakatau,
necklace; hakatautau, to append. 5. Anchor;
kona tau, anchorage, port. 6. To fight;
hakatau, challenge, to defy, to incite;
hakatautau, to rival. Churchill.
The Malay word for 'year' is
taun or tahun. In all Polynesian dialects
the primary sense is 'a season', 'a period of time'.
In the Samoan group tau or tausanga,
besides the primary sense of season, has the
definite meaning of 'a period of six months', and
conventionally that of 'a year', as on the island of
Tonga. Here the word has the further sense of 'the
produce of the year', and derivatively 'a year'. In
the Society group it simply means 'season'. In the
Hawaiian group, when not applied to the summer
season, the word keeps its original sense of 'an
indefinite period of time', 'a life-time, an age',
and is never applied to the year: its duration may
be more or less than a year, according to
circumstances. So far our authority (Fornander, I,
124; cp. 119). It seems however to be questionable
whether the original sense is not the concrete
'produce of the seasons', rather than the abstract
'period of time'. It is significant that on the
Society Islands the bread-fruit season is called
te tau, and the names of the other two seasons,
te tau miti rahi and te tau poai, are
formed by adding to this name. Nilsson.
At the
risk of invoking the criticism, 'Astronomers rush in
where philologists fear to tread', I should like to
suggest that Taku-rua corresponds with the
two-headed Roman god Janus who, on the first of
January, looks back upon the old year with one head
and forward to the new year with the other, and who
is god of the threshold of the home as well as of
the year... There is probably a play on words in
takurua - it has been said that Polynesian
phrases usually invoke a double meaning, a common
and an esoteric one. Taku means 'slow', the
'back' of anything, 'rim' and 'command'. Rua
is a 'pit', 'two' or 'double'. Hence takurua
has been translated 'double command', 'double rim',
and 'rim of the pit', by different authorities.
Taku-pae is the Maori word for 'threshold'...
Several Tuamotuan and Society Islands planet names
begin with the word Takurua or Ta'urua
which Henry translated Great Festivity and which is
the name for the bright star Sirius in both New
Zealand and Hawaii. The planet names, therefore,
represent the final stage in the evolution of
takurua which was probably first applied to the
winter solstice, then to Sirius which is the most
conspicious object in the evening sky of December
and January, and was then finally employed for the
brilliant and conspicious planets which outshone
even the brightest star Sirius. From its association
with the ceremonies of the new year and the winter
solstice, takurua also aquired the meaning
'holiday' or 'festivity'. Makemson |
The year was
anciently two 'years' (half-years or periods somewhat shorter
due to the invisibility of the Pleiades or other stars).
Therefore taku-rua (ta'u-rua, tau-rua,
two 'stones'), the foundation of the system of balls and rhombs.
Triple 'stones'
with a 'notch' would be a good picture for the Belt of Orion, a
marker for new year. The three islets outside Orongo
would be connected with the Belt of Orion and with the beginning
of a new year.
Triple rhombs
would serve as the opposite side of the year, when sun ruled
over the land. At night (winter) new year is inaugurated by
admiring Orion (or the Pleiades), while the changing status of
the sun is only to be seen in the daytime.
Is it possible
to get any confirmation of these ideas from the glyphs in
Tahua? Let us begin by listing all GD53 glyphs:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
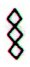 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
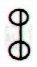 |
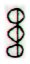 |
 |
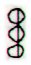 |
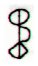 |
8 * 6 +
4 = 52 on side b (above) and 9 * 6 = 54 on side a
(below) |
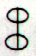 |
 |
 |
 |
 |
 |
 |
 |
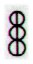 |
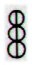 |
 |
 |
 |
 |
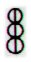 |
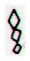 |
 |
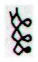 |
 |
 |
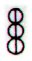 |
 |
 |
 |
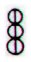 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
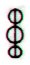 |
 |
 |
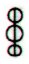 |
 |
 |
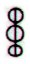 |
 |
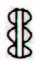 |
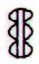 |
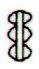 |
 |
 |
 |
 |
 |
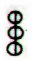 |
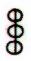 |
 |
Curiously we
have 52 (= 4 * 13) glyphs on side b and 54 (= 3 * 18) on side a.
Is this really coincidence? I have not (consciously) manipulated
the numbers. There are 52 cards in a deck of cards, plus two
Jokers.
Next, we delete
the ball glyphs to isolate the rhomb glyphs:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
5 * 6 =
30 on side b (top) and 8 on side a (bottom) |
The number of
rhomb glyphs (30 respectively 8) could suggest that the hypothesized
link between rhombs and sun is a correct assumption.
| |
side b |
% |
side a |
% |
|
rhomb
glyphs |
30 |
56 |
8 |
15 |
|
ball
glyphs |
24 |
44 |
44 |
85 |
|
sum |
54 |
100 |
52 |
100 |
Unquestionably
there is a message telling us about how on side a there are very
few rhombs, a fact we should contrast with how we earlier
have found side a to be 'in the light from the sun', while side
be still is in the dark. But we must be more precise about the
distribution of the rhomb glyphs. Are they located before or
after the middle of respective side?
 |
 |
 |
 |
 |
 |
|
Ab2-45 |
Ab3-50 |
Ab5-7 |
Ab5-37 |
Ab5-39 |
Ab5-41 |
 |
 |
 |
 |
 |
 |
|
Ab5-48 |
Ab5-50 |
Ab5-52 |
Ab5-55 |
Ab5-58 |
Ab5-67 |
 |
 |
 |
 |
 |
 |
|
Ab5-68 |
Ab5-80 |
Ab6-2 |
Ab6-38 |
Ab6-39 |
Ab6-40 |
 |
 |
 |
 |
 |
 |
|
Ab6-66 |
Ab6-67 |
Ab6-69 |
Ab6-70 |
Ab6-72 |
Ab6-73 |
 |
 |
 |
 |
 |
 |
|
Ab6-74 |
Ab6-75 |
Ab6-88 |
Ab6-90 |
Ab7-27 |
Ab7-62 |
 |
 |
 |
 |
 |
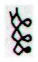 |
|
Aa1-78 |
Aa1-84 |
Aa2-45 |
Aa4-1 |
Aa4-69 |
Aa5-8 |
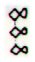 |
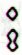 |
Redmarked
glyphs are located in lines 1-4, the rest (blue) are in lines 5-8. |
|
Aa6-82 |
Aa8-80 |
Rhomb glyphs (as
a rule) are not located among the glyphs in the first half of
respective side. A new table summarizes the exact figures:
|
number
of rhomb glyphs |
|
line no. |
side b |
side a |
line no. |
side b |
side a |
|
1 |
- |
2 |
5 |
12 |
1 |
|
2 |
1 |
1 |
6 |
14 |
1 |
|
3 |
1 |
- |
7 |
2 |
- |
|
4 |
- |
2 |
8 |
- |
1 |
|
sum |
2 |
5 |
sum |
28 |
3 |
The red-marked numbers (for the 2nd half of side b) do not look
random and appear to be a result of the design of the creator.
|