|
TRANSLATIONS
The hyperlink to an explanation of how the numbers 84 and 96 were arrived at, leads to these pages:
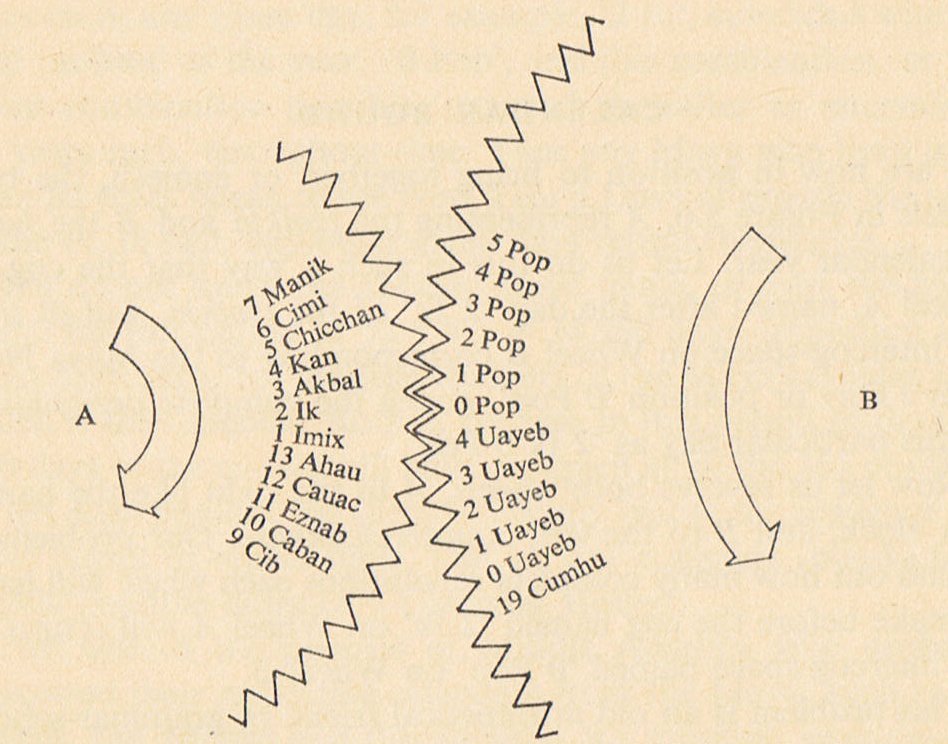
6 instead of 8 'winter' months means 'sun' instead of 'moon. The winter (moon) north of the equator becomes summer (sun) south of the equater. Changing from 20 day winter months (Maya) to 28 night months (Easter Island) harmoniously suggests changing from 'sun' to 'moon'. 8 (moon) * 20 (sun) is changed to 6 (sun) * 28 (moon). But the Mayas had the same length for their months all over the year (excepting Vayeb). Maybe this fact convinced the Easter Island calendar creators to chose 16 for summer, a number which combines sun and moon, because the growing moon is the result of new moon having met with the sun and been radiated all over: ...when the new moon appeared women assembled and bewailed those who had died since the last one, uttering the following lament: 'Alas! O moon! Thou has returned to life, but our departed beloved ones have not. Thou has bathed in the waiora a Tane, and had thy life renewed, but there is no fount to restore life to our departed ones. Alas'... 192 is also the number of glyphs in K, which I earlier have reconstructed as *97 + *95. Earlier I have furthermore suggested that the K text cannot cover the whole year, only the summer half. The reoccurrence of 192 for the number of summer days (in the deduced kuhane calendar) is a fact which strengthens my reconstructed number of glyphs in K. And vice versa, of course, meaning that the reconstructed number of glyphs in K implies a probable common view shared between the creator of the K text and the creators of the kuhane story. In G the 32 periods of summer is a construction similar to the 32 days for each of the 6 summer months according to the proposed kuhane calendar. Given a common view, each G period will be 6 days long, a good number implying sun of course. 168 for the number of nights in winter is also a number we recognize from the rongorongo texts:
354 was also the result of my counting on the skirt of Pachamama. 168 + 186 = 354 = 6 * 59 (sun combined with moon), to be compared with 168 + 192 = 360. Maybe the Pachamama creators thought along similar lines (as the Easter Islanders) in extending winter from 2 * 80 to 2 * 84 nights. Also they lived south of the equator. Instead of prolonging summer with a compensating 8 days they seem, however, to have decided for extedning summer with only 2 days, thereby establishing a year with exactly 12 lunar months. According to my reconstruction of the kuhane calendar, there should be a division into three + three equally long months (with 28 nights each) before and after new year, not a divison into halves (as I thought earlier when counting glyphs in E). The cycle turns around beyond Eb6-17 and starts again with Eb1-37:
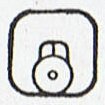
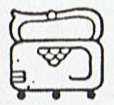
19 - 4 = 15 (b6) + 6 (b1) = 21. 26 - 21 = 5, i.e. Eb2-6. 27 - 7 = 20 (b2). 26 - 20 = 6 (b3), i.e. Eb3-7. Why did I not arrive at Eb3-7 when earlier counting halves? 35 - 11 = 24 (b5) + 16 (b8) = 40. 19 - 18 = 1 (b6) + 6 (b1) + 27 (b2) = 34. 40 - 34 = 6 (b3), i.e. Eb3-7. A mistake was done earlier. I have not scrutinized the glyph dictionary pages beyond hua poporo yet. Interesting is the appearance of haga rave in Eb2-7, corresponding to what looks as the beginning of Hatiga Te Kohe:
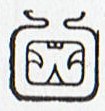
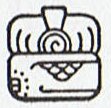
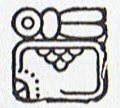
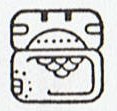
But possibly Hatiga Te Kohe is what Eb2-6 illustrates, and Akahaga what Eb2-7 illustrates. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||