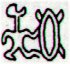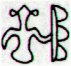|
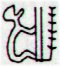
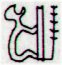
6. A mirror event has evidently been drawn in Gb8-2 compared to Ga5-3, with henua open at bottom respectively at the top and once again number 142 pops up:
142 is not an obvious Sign, but the distance from Achird to Regulus maybe could explain its importance. Perhaps 364 - 142 = 222 (100 more than 122) refers to the number of days in summer. We have met number 222 earlier, for instance as the day number of Toliman (α Centauri), cfr e.g. at The Crocket Ground. Leo is an ancient constellation and once, north of the equator, it could defend its place in the sky because a lion was the obvious Sign for the ruler of 'land'. The Lion is the king among the animals. Its place must be in summer. At the other end of the sky is Aquarius, the constellation in 'water'. Since that time Regulus has moved to the same place south of the equator - its heliacal rising means winter ('water') no longer rules. The ancient signs in the sky could be reused. Within a month after the return of Regulus spring equinox would be there:
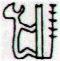
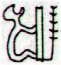
We can compare Ga5-5 with Ga5-10:
These glyphs seem to express opposites because the 'sails' are at left in Ga5-5 but at right in Ga5-10. However, the signs connected with the 'sails' are probably opposites in meaning and therefore there is a double negation which should imply the glyphs are expressing similar events. From 122 to 266 there are 144 days, a square of Sun (12), which could mean there is an end to spring equinox at viri in Ga5-11. Maybe the glyph refers to 'the nakshatra spring equinox', i.e. to how an observer north of the equator can deduce that sun is at spring equinox from seeing full moon in Regulus. North of the equator spring equinox arrives later than after 87 days.
There are 186 days from autumn equinox to spring equinox instead of 179, and the difference is about the same as the number of glyphs from Ga5-5 to Ga5-11. With autumn equinox as day number 266 both north and south of the equator it would be rational to let the difference in length be expressed at the end of winter. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||