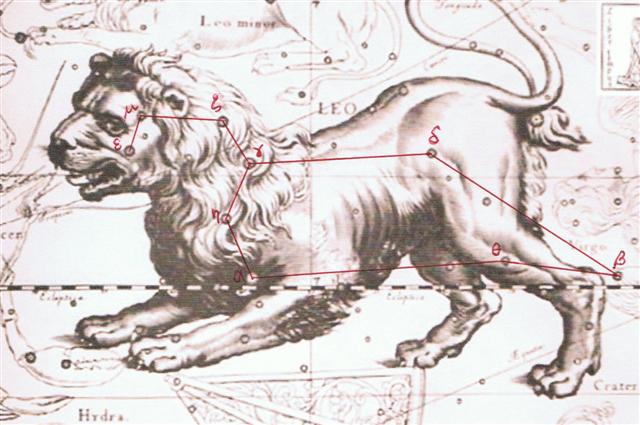
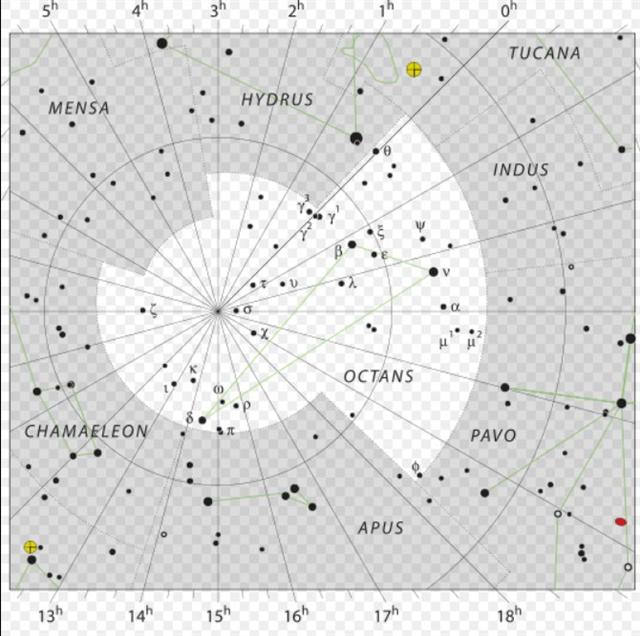
In other words, as viewed from a place south of the equator - such as Easter Island - the corresponding (nakshatra) place in the year to observe for the Full Moon should be half a year away in February 23 (anciently the date for Terminalia).

... The leap day was introduced as part of the Julian reform. The day following the Terminalia (February 23) was doubled, forming the 'bis sextum - literally 'double sixth', since February 24 was 'the sixth day before the Kalends of March' using Roman inclusive counting (March 1 was the 'first day') ...

This explains why the beginning of the retrograde cycle of Mars was indicated as August 23, i.e. when Mars would be visible in the night sky close to the Pleiades.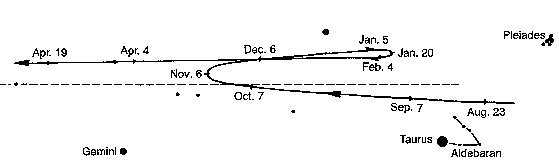

In my documentation a complication is how to present the place for Mars in AD 2023 when the G text evidently was created with the intent to have the northern spring equinox in the era of the Golden Bull at the beginning of side a on the tablet.

We can see that day 378 (JANUARY 13) was located at glyph number 298 (= 378 - 80), which place - at the tail of the southern of the pair in Fishes (Pisces) - according to the era of Bharani should have arrived 64 - 41 = 23 days later in the year, viz. in day 378 + 23 = 401 ("February 5, 31 + 5 = 36 = 401 - 365). And according to my assumed era for rongorongo the precession would then have carried the Sun a further 41 (= 64 - 23) days ahead in the Gregorian calendar, to day 401 + 41 = 442 (= 365 + 77), viz. to March 18 (*362 = 442 - 80).

Where should I put the place for the planet Mars when it had been visible in the nakshatra night (at the Full Moon) position in August 23 AD 2023? The precession since the era of rongorongo is no major problem, but the cycle of Mars implies it will move ahead among the fixed stars with around 50 (= 780 - 2 * 365) days for every year.

I have chosen to ignore this problem for the moment and to simply tell about which current observation year (for the planet Mars) the day August 23 is referring to. But it seems reasonable to assume the creator of the G text 'discounted' *361.4 (the right ascension day according to my assumed year for rongorongo) down to the era of Bharani, a star which at that time had been located at *41.4, because this operation would transform *361.4 to *320.0 (i.e. the right ascension line connected to the south pole star Dramasa, σ Octantis).

... Greek sigma therefore resembles Cassiopeia in between, when she was in the west at the time when the Sun was rising in the east ...

In March 17 (the place in the Gregorian calendar corresponding to when in my assumed era for rongorongo the Sun would have risen at the right ascension line at γ¹ Octantis) the Full Moon would ideally be half a year away at the place for September 15 (31 + 28 + 17 + 182 = 258, *178).

In September 15 (according to my assumed era for rongorongo) the triplet of stars - 93 Leonis, Denebola, Alaraph - and the planet Mars would all have been together at the Sun, and south of the equator, on Easter Island, the star observers should therefore have looked in the night for the corresponding place for the Full Moon at the place for March 17:

A year earlier on the other hand, in August 23 AD 2022, the place for the planet Mars had been in Taurus not far from the Pleiades (M45):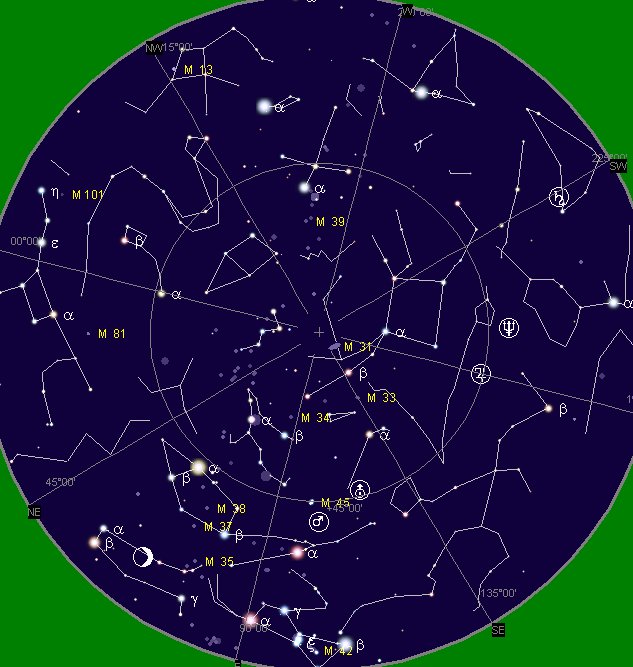

And two years later, in August 23 AD 2025, the planet Mars ought to be around 780 - 2 * 365 = 50 days after September 15 (258), viz. around November 4 (308). Or to be more precise: 780 - 2 * 364 = 52 days after September 15 (258), viz. in November 6 (which indeed is noted in the retrograde diagram above as a turning point for Mars).

... Another name for Mercury was Hermes and Hermes Trismegisthos (thrice-mighty) could have referred to the fact that there were 3.141 * 115.88 = 364.0 days for the cycle of the Earth around the Sun. Although the calendar has 365 days for a year this is due to the fact that the Earth has to turn around an extra day in order to compensate for how the direction to the Sun changes during a year ...