407. But there is a problem: ... The precessional distance down from the time of rongorongo to that of the First Father can be calculated as around (1842 + 3112) / 26000 * 365.25 = 70 right ascension days, or as 6 days more than 64 = 10 days less than 80. It was evidently Polaris who rose with the Sun when Hun-Nal-Ye became the sky, and it would have been in day 392 (January 26) - 10 = 382 (January 16) when the companion star of Polaris (*26.6), viz. the Belly of the Fish (Baten Kaitos, ζ Ceti, *26.6) would have returned to visibility after the close encounter with the Sun in December 31. Polaris never sank below the horizon and it was therefore outside the cycles of heliacal risings and settings ...
Because according to Allen Polaris did not attain status as north pole star until Roman times:
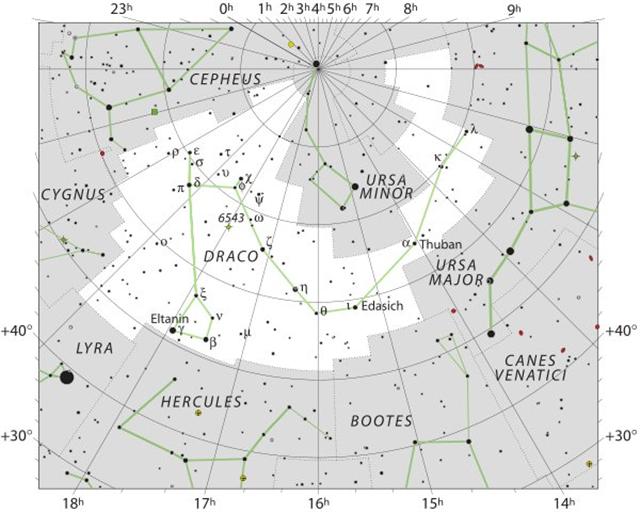
"... it should be remembered that during many milleniums the polar point has gradually been approaching our pole-star, which 2000 years ago was far removed from it, - in Hipparchos' time 12º 24' away according to his own statement quoted by Marinus of Tyre and cited by Ptolemy. Miss Clerke writes as to this: The entire millenium before the Christian era may count for an interregnum as regards Pole-stars. Alpha Draconis had ceased to excercise that office; Alruccabah had not yet assumed it ..."
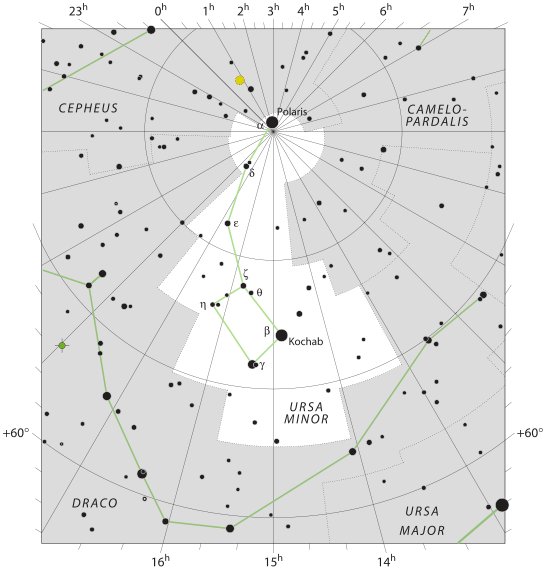
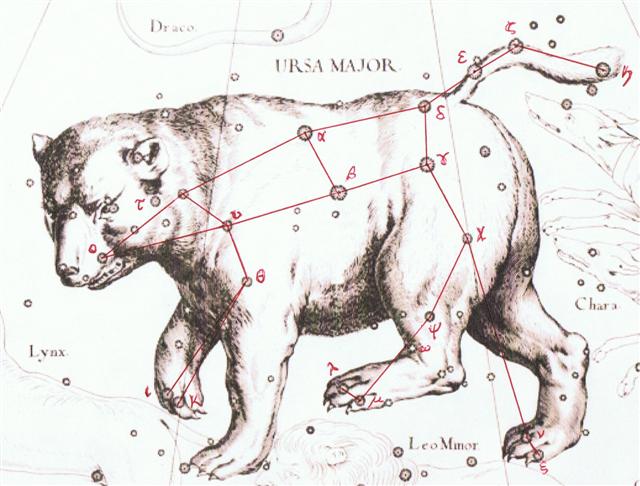
The term Alruccabah may have referred first to Kochab (Kakkab, Star, *225.0) before being applied to Polaris, because - as we can see above - Kochab would have been a natural choice when Thuban (*212.8) became outdated. "Alrucaba, or Alruccaba, which probably should be Al Rukkabah, is first found in the Alfonsine Tables, although the edition of 1521 applied it only to the lucida. While this generally is supposed to be from the Arabic Al Rakabah, the Riders, Grotius asserted that it is from the Chaldee Ruku, a Vehicle, the Hebrew R'khūbh; and, if so, would seem to be equivalent to the Wain and from the Hebrew editor of Alfonso. Others have thought it from Rukbah, the Knee, as β always has marked the forearm of the Bear, and Alrucaba, in a varied orthography, was current for that star some centuries ago, as it is now for Polaris ..." (Allen) When Itzam-Yeh was referred to as Ursa Major, rather than to a particular star, it could be a similar phenomenon, viz. to use the name of the whole figure revolving up in the far north.
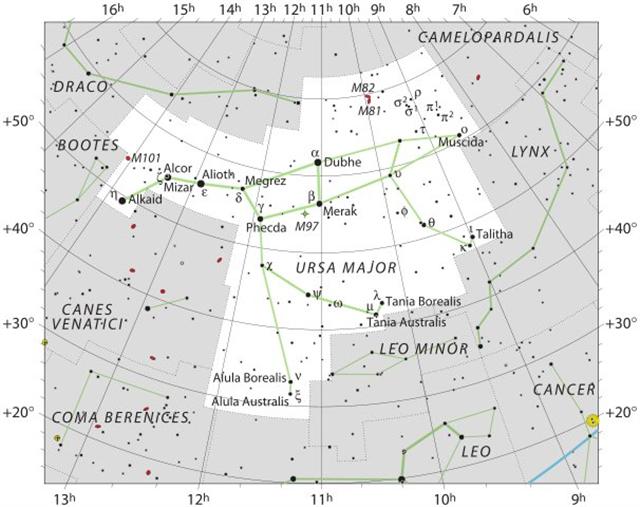
It could have begun when Alioth (ε Ursae Majoris, 'Fat Tail') was at the north pole.
Hun-Nal-Ye could then have initially referred to Kochab (*225.0) in Ursa Minor, a star close to the right ascension line of Bharani (*41.4) - although we have then to assume this line to continue beyond the north pole. *41.4 + *365.25 / 2 = *224.0.
At the time of Bharani (14.8 precessional days before Baten Kaitos and Polaris) the time of Ursa Major was definitely in the past. Maybe Itzam-Yeh was finished already in day 148:
The creation of our present world took place in day 225 (alluding to *225 at Kochab) and this was 12 weeks after the first 3-stone place. The right ascension time lines did not apply to stars close to the north pole and only by connecting them with some star farther down could they (in a way) be dated. ... The story of Rip Van Winkle is set in the years before and after the American Revolutionary War. Rip Van Winkle, a villager of Dutch descent, lives in a nice village at the foot of New York's Catskill Mountains. An amiable man whose home and farm suffer from his lazy neglect, he is loved by all but his wife. One autumn day he escapes his nagging wife by wandering up the mountains. After encountering strangely dressed men, rumored to be the ghosts of Henry Hudson's crew, who are playing nine-pins, and after drinking some of their liquor, he settles down under a shady tree and falls asleep. He wakes up twenty years later and returns to his village. He finds out that his wife is dead and his close friends have died in a war or gone somewhere else. He immediately gets into trouble when he hails himself a loyal subject of King George III, not knowing that in the meantime the American Revolution has taken place. An old local recognizes him, however, and Rip's now grown daughter eventually puts him up ... ... The story is a close adaptation of Peter Klaus the Goatherd by J.C.C. Nachtigal, which is a shorter story set in a German village. The story is also similar to the ancient Jewish story about Honi M'agel who falls asleep after asking a man why he is planting a carob tree which traditionally takes 70 years [Sic!] to mature, making it virtually impossible to ever benefit from the tree's fruit. After this exchange, he falls asleep on the ground and is miraculously covered by a rock and remains out of sight for 70 years. When he awakens, he finds a fully mature tree and that he has a grandson. When nobody believes that he is Honi, he prays to God and God takes him from this world. Note also that the family name of Honi is also a term of geometry ('M'agel' is Hebrew for 'circle maker'), as well as the family name of Rip ('Winkel' is German for 'angle'). The story is also similar to a 3rd century AD Chinese tale of Ranka, as retold in Lionel Giles in A Gallery of Chinese Immortals. In Orkney there is a similar and ancient folklore tale linked to the Burial mound of Salt Knowe adjacent to the Ring of Brodgar. A drunken fiddler on his way home hears music from the mound. He finds a way in and finds the trowes (Trolls) having a party. He stays and plays for two hours, then makes his way home to Stenness, where he discovers fifty years have passed. The Orkney Rangers believe this may be one source for Washington Irving's tale, because his father was an Orcadian from the island of Shapinsay, and would almost certainly have often told his son the tale. The original story was by Diogenes Laertius, an Epicurean philosopher circa early half third century, in his book On the Lives, Opinions, and Sayings of Famous Philosophers. The story is in Chapter ten in his section on the Seven Sages, who were the precursors to the first philosophers. The sage was Epimenides. Apparently Epimenides went to sleep in a cave for fifty-seven years. But unfortunately, 'he became old in as many days as he had slept years'. Although according to the different sources that Diogenes relates, Epimenides lived to be one hundred and fifty-seven years, two hundred and ninety-nine years, or one hundred and fifty-four years. A similar story is told of the Seven Sleepers of Ephesus, Christian saints who fall asleep in a cave while avoiding Roman persecution, and awake more than a century later to find that Christianity has become the religion of the Empire ...
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||