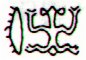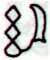In H, with 3 glyphs per day,
glyph lines a9 and b9 maybe could be
used.
Next page:
|
Next we ought to look at koti at Ca9-9:
 |
 |
 |
 |
 |
 |
|
Ca3-12 |
Ca7-24 |
Ca9-9 |
Cb6-6 |
Cb6-22 |
Cb14-8 |
First, however, we will have a
quick look at a pair of useful manu kake. They will e.g. help us understand why there are so many glyphs on side a (392)
compared to side b (348). The area to write on is equally large on
side b, and therefore the designer of the C text must have had a purpose
in determining this distribution of the glyphs:
|
side
a |
side
b |
|
392 |
102 |
 |
240 |
 |
4 |
|
Cb5-9 |
Cb14-15 |
|
103 |
344 |
At first only 240 (= 10 * 24 = 30 *
8) appears to be of possible significance. Twisting and turning the
numbers in the table above, in order to look for more interesting
alternatives, this will then emerge:
|
392 |
102 |
 |
240 |
 |
4 |
|
Cb5-9 |
Cb14-15 |
|
495 = 5 * 99
= 5 * (50 + 49) |
245 = 5 * 49 |
|
250 + 2 *
245 = 740 |
Cb5-9 divides the
text so that there will be 245 (5 times 7 squared) glyphs beyond it
to the end of side b. The other part, which includes Cb5-9 itself,
is 495 (5 times 99) glyphs long, a number which in turn is possible
equate with 250 + another 245.
I do not believe these numbers are
arbitrary, instead they reveal a design. For instance, it
is possible to 'read' 245 as short for 24 times 5 = 120, and twice
245 will then be twice 120 = 240. More
arguments - relevant for koti at Ca9-9 (once again a double 9)
- will be presented following this link.
|
There is one more manu kake
in C, towards the end of side a:
We can try to add it to the picture:
|
388 |
 |
3 |
102 |
 |
240 |
 |
4 |
|
*Ca14-26
(389) |
Cb5-9 |
Cb14-15 |
|
495 |
245 |
|
740 |
392 persists, it now
becomes the number of glyphs between Cb14-15 and Ca14-26. These
numbers seem to be significant: 14 * 15 = 210 = 7 * 30 and 14 *
26 = 364 = 7 * 52.
740 -
210 = 530.
364 -
210 = 7 * 22 = 154.
388 -
210 = 178, and if we add 4 we will reach 182.
392 = 182 + 210. With
14 * 26 = 364 it could mean there are 182 days ending at
Ca14-26.
389 -
182 = 207, which is the ordinal number of Ca8-8:
 |
 |
 |
 |
|
Ca8-4 |
Ca8-5 |
Ca8-6 |
Ca8-7 |
 |
 |
 |
|
Ca8-8 |
Ca8-9 |
Ca8-10 |
This
solution to the problem does not seem to be very promising. Only
8 * 8 = 64 is obviously significant.
Another way is to use our experience
of earlier manu kake glyphs,
for instance the connection between
104, 260, and 364:
|
364 |
4 * 26 =
104 |
10 * 26 =
260 |
14 * 26 |
 |
258 |
 |
|
Ga4-21 (105) |
Gb5-10 (364) |
|
260 |
If 364 suggests 260, then we can
guess the ordinal number for Ca14-26
should be 105.
389 - 105 = 284, which coincides
with the end of line Ca10:
 |
 |
 |
 |
 |
 |
 |
|
Ca10-22 |
Ca10-23 |
Ca10-24 |
Ca10-25 |
Ca10-26 |
Ca10-27 |
Ca10-28 |
 |
 |
 |
 |
|
Ca10-29 (284) |
Ca11-1 |
Ca11-2 |
Ca11-3 |
 |
 |
 |
 |
 |
 |
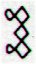 |
|
Ca11-4 |
Ca11-5 |
Ca11-6 |
Ca11-7 |
Ca11-8 |
Ca11-9 |
Ca11-10 |
This seems to be promising - Rogo
is present - but quite too difficult
for the moment. We should wait with
this section of the text until
kara etahi.
Let me just add that
Ca10-29 does not agree with number
284, and one way to interpret this
incongruence is to say that counting
should begin 6 glyphs earlier than
with Ca1-1. It gives interesting
results:
 |
 |
 |
 |
 |
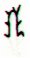 |
|
Cb14-14 |
Cb14-15 |
Cb14-16 |
Cb14-17 |
Cb14-18 |
Cb14-19 |
| 1 |
2 |
3 |
4 |
5 |
6 |
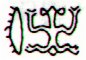 |
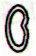 |
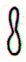 |
 |
 |
| Ca3-9 |
Ca3-10 |
Ca3-11 |
Ca3-12 |
Ca3-13
(63) |
| 65 |
66 |
67 |
68 |
69 |
 |
 |
 |
| Ca3-14
(64) |
Ca3-15 |
Ca3-16 |
| 70 |
71 |
72 |
At the other end of this solution we
can search for day (glyph) number
364. Note 36 and 4 in harmony with
28 and 4.
284 + 364 = 648 (a
good number, hinting at 8 * 8 eight
times). Also, 648 = 348 (number of
glyphs on side b) + 300.
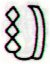
648 - 392 = 256 (= 4
* 64). The searched for glyph is
Cb11-4 (number 252 + 4 on side b):
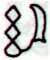 |
 |
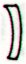 |
 |
 |
 |
|
Cb11-3 |
Cb11-4 (648) |
Cb11-5 |
Cb11-6 |
Cb11-7 |
Cb11-8 |
 |
 |
 |
 |
 |
 |
|
Cb11-9 |
Cb11-10 |
Cb11-11 |
Cb11-12 |
Cb11-13 |
Cb11-14 |
 |
 |
 |
 |
 |
 |
|
Cb11-15 |
Cb11-16 |
Cb11-17 |
Cb11-18 |
Cb11-19 |
Cb11-20 |
 |
 |
 |
 |
 |
 |
|
Cb11-21 |
Cb11-22 |
Cb12-1 |
Cb12-2 |
Cb12-3 |
Cb12-4 |
We can set up a hypothesis:
 |
104 |
 |
258 |
 |
|
Ca10-29 (284) |
*Ca14-26 (389) |
Cb11-4 (648) |
|
4 * 26 |
10 * 26 |
Rogo at Ca10-29 will be the
last glyph of the preceding season.
740 - 364 = 376 and 376 - 284 = 92,
which must be Cb11-5. 92 - 74 = 18,
and 22 - 4 = 18:
|
a1 |
26 |
26 |
b1 |
24 |
348 |
24 |
|
a2 |
25 |
51 |
b2 |
25 |
324 |
49 |
|
a3 |
25 |
76 |
b3 |
22 |
299 |
71 |
|
a4 |
29 |
105 |
b4 |
23 |
277 |
94 |
|
a5 |
35 |
140 |
b5 |
21 |
254 |
115 |
|
a6 |
28 |
168 |
b6 |
29 |
233 |
144 |
|
a7 |
31 |
199 |
b7 |
27 |
204 |
171 |
|
a8 |
29 |
228 |
b8 |
29 |
177 |
200 |
|
a9 |
27 |
255 |
b9 |
30 |
148 |
230 |
|
a10 |
29 |
284 |
b10 |
22 |
118 |
252 |
|
a11 |
32 |
316 |
b11 |
22 |
96 |
274 |
|
a12 |
27 |
343 |
b12 |
25 |
74 |
299 |
|
a13 |
20 |
363 |
b13 |
30 |
49 |
329 |
|
a14 |
29 |
392 |
b14 |
19 |
19 |
348 |
|
sum |
392 |
sum |
348 |