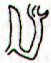Suppose the E calendar (with those 24 periods ending with kiore+henua glyphs) covers the first half of the year - when the 'rat' is seen climbing higher in the cosmic tree - then we have a connection with the K text, because 192 = 8 * 24. Possibly, therefore, each of the 24 periods in E covers 8 days.

If so, then we should turn our earlier idea about the structure of the K calendar (viz. a 'net' with 'meshes' equal to 24 days) upside down. The 3 'limbs' of spring would be 192 / 3 = 64 days long (not possible if we have 24-day periods, because 64 / 24 = 2 ⅔).

192 = 8 * 8 + 8 * 8 + 8 * 8, a nice patten with 6 elements. Of course, it could be expressed differently, e.g. as 192 = 4 * 16 + 4 * 16 + 4 * 16. Or as 2 * 32 + 2 * 32 + 2 * 32.

Examining the different variants of kiore+henua in E we can see that 22-23 have 'ghostly status', while 7 and 12 still are 'living' although their feet have lost contact with the ground:

1	2	3	4	5	6
7	8	9	10	11	12
13	14	15	16	17	18
19	20	21	22	23	24

Possibly the two 'ghosts' explain the other key number in K, viz. 24 - 2 = 22.

If the E pattern can be applied for measuring the 'meshes' in K, then we need not worry until we arrive at position 192 - 3 * 8 = 168:

Kb4-11	Kb4-12	Kb4-13	Kb4-14
Kb4-15 (168)	Kb4-16	Kb4-17	Kb4-18

Then comes 3 last periods with (possibly) the pattern 7, 8, 9:

7
	Kb4-15 (168 = 6 * 28)	Kb4-16	Kb4-17	Kb4-18
		...
	Kb4-19	Kb5-1	Kb5-2 (174 = 6 * 29)	Kb5-3
8
	Kb5-4	Kb5-5 (177 = 6 * 29.5)	Kb5-6	Kb5-7
	...			...
	Kb5-8	Kb5-9	Kb5-10 (182 = 6 * 30⅓)	Kb5-11
9
	Kb5-12	Kb5-13	Kb5-14	Kb5-15
	Kb5-16	Kb5-17	Kb5-18	Kb5-19
	Kb5-20 (192 = 6 * 32)

The results are reassuring. We can identify Nga Kope Ririva at Kb5-5 ('fire-fire'), where henua has the 'night' ('moon') sign at its top. In Kb5-2 (5 * 2 = 10) a normal great henua is located at 6 * 29, and at Kb5-10 (5 * 10 = 50 = half 100) the ordinal number is half 364. The force of the pattern enables us to decipher 168 and 192 in a new way (probably the proper way in this context):

I have redmarked those numbers which appear to carry most weight. We can for instance now map the kuhane stations, using the last of them in the light of the sun (6) - viz. the three islets - as a firm point, and from there move backwards (in space) = forwards (in time):

I find Te Pu Mahore important. It proves that we have to move backwards in time on side a of G and all the way through the K text.

Kb3-9 obviously has a hole (pu) and I have redmarked this glyph because it is the only one in the table above which obviously and definitely can connect one of the kuhane names with a glyph. Earlier I still nourished a little doubt if really the kuhane stations on side a of G could be read in the order I have proposed:

I have redmarked also the name Nga Kope Ririva, because I find it to be a secure fixed point to stand on.

But we cannot be sure that we can read side a of K without changing direction. Should we change Te Manavai into Te Piringa Aniva and the other way around?

Te Piringa Aniva
	Ka5-4	Ka5-5	Ka5-6 (89)	Ka5-7	Ka5-8
Te Kioe Uri
	Ka3-11	Ka3-12	Ka3-13 (59)	Ka3-14	Ka3-15
Te Manavai
	Ka2-4	Ka2-5	Ka2-6 (30)	Ka2-7	Ka2-8

No, I doubt it. The story according to the glyphs in G has its parallel in the text of K, and time goes according to the multiples of 29.5 - probably in reversed order on side a of G and on both side of K.

If we should reverse the time order on side a of K to be the opposite of its side b, we ought to begin counting multiples of 29.5 from the end of side a (of K) instead of from its beginning. The reversed time order on side a of G would then be parallel with the reversed time order on side b of K - but not with the order on side a of K. On side a of K a non-reversed time order would rule. Two negations makes a positive statement.