|
TRANSLATIONS
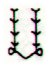
These are the 9 glyphs:
As a first step we should renumber Hb8-114 and Hb8-136 to establish their original numbers in the glyph line. I have earlier counted the number of glyphs in line b8 as *54:
We will now count once more. There is no problem with the first 15 glyphs:
Then comes a question mark, because there could, at least theoretically, once have been a glyph between Hb8-15 and Hb8-101:
But when I earlier thought about this, I decided there was no glyph missing:
It is quite possible that the creator of H left an empty space to the right of Hb8-15 (where 8 * 15 = 120), a glyph which is drawn open to the right. This empty space (if it was designed to be there) should not be counted, I guess. I see no reason to change my earlier judgment. Therefore we can assign the (probably) correct original ordinal numbers in line Hb8:
Next, we should count from Ha1-1. If we can trust my table over number of glyphs per line (above), then the result will be:
I have redmarked Ha5-18 (which we already know) and two glyphs which seem to be rather close in character. Hb8-30 and Hb9-1 are twins with wings are drawn to be different. The rest of the glyphs have other and more obvious signs. Now we count. A first suggestion which quickly emerged:
3 glyphs per day is maybe a basic trait in the H text. 540 = 3 * 180 could be half a year. Increasing 750 to 756 then gives 3 * 252. And 252 = 7 * 36, a good number. This solution could begin with:
We should notice that Hb7-38 is our special honui glyph (of the ariga erua kind). It comes 6 glyphs (2 days?) beyond Hb7-32:
But there are of course three different ways to structure 3 glyphs together into one day. If there are 3 glyphs per day, then 648 glyphs = 216 days, and the whole text will be 2 * 216 = 432 days long (= 12 * 36 days). Day 329 ends with Hb7-32 (according to my guess). 32 * 9 = 288 = 8 * 36. 7 * 32 = 224 = 8 * 28. At Hb7-38 we can count 7 * 38 = 266, the number of Te Pou (= 9 * 29.5 = 265.5). Advancing from day 330 (day 1), taking triplets of glyphs for each day, we will reach day 180 after 540 glyphs:
232 (at Ha5-16) is glyph number 540 counted from Hb7-33 (989). 988 + 540 - 1296 = 232:
The suggested system of triplets of glyphs seems to break down because of such glyphs as Ha5-7 and Ha5-13 (redmarked above). Once again we find 5-7 at a special glyph. And neither is the quartet Ha5-17--20 congruent. But if we combine all the redmarked glyphs they can stand for 2 days (= 182 - 180). And we had 2 glyphs (days) intercalated at the beginning of side b of G:
This solution has 180 + 2 days following Hb7-32, which - we can assume - is at winter solstice (the person has sunken down up to his neck). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||