|
TRANSLATIONS
Once upon a time, in the Old World (meaning continental Eurasia), it was clear that Cosmos (time-space) was formed like a hexagonal star:  ... On the day when Tīstar produced the rain, when its seas arose therefrom, the whole place, half taken up by water, was converted into seven portions; this portion, as much as one-half, is the middle, and six portions are around; those six portions are together as much as Khvanīras ... We now can understand that when Tistar produced rain in quantity enough to drench half the world, the deluge, it collected in the central hexagon, while only the mountains (6 of them) remained dry. The old Babylonian view saw only sea in the south and mountains in the north. During the deluge the low part became filled with water and the fires went out, of course. In the north the problem was not, fires still burned. Their Cosmos implied that winter, night, inside, water etc had in common the absence of fire. The view spread to ancient China, where a sophisticated system of correlations measured out the whole world accordingly. It also spread to ancient Europe, and still in the time of Captain Cook it was believed that half the world was covered by ocean, mostly in the south. But calculations had shown that there must be unknown lands south of the equator, because there was more water than land in the known atlas. Terra Australis Incognita it says on the map engraved on my table (where Australia is located, not yet discovered when Captain Cook was sent out to investigate). Women should be inside the houses and men outside in the sun light. Men should stand high like mountains, women should lie down low. The stern men came first (1), the weeping women behind (2), their faces hidden of course. There once were only 6 zodiacal constellations. Time was counted by the phases of the moon. Double-months were necessary because 29.5 could not be understood by common man. I cite myself from the very beginning (Level 1) of this long journey: ... In the beginning the methods of counting did not manage more than whole positive numbers. Therefore it was very inconvenient that the period of the phases of the Moon took more than 29 days but less than 30. Keeping order in the calendar for the Moon required some kind of trick. The trick established all over the ancient world (as I guess) was to count two periods, because with 59 days the problem was solved. The revolution of the phases of the Moon is very nearly 29 ½ days. And day no. 60 then became the first day of the new double-moon period. The Sumerians therefore had the same sign for 60 as for 1. Zero was not yet invented and there could be no misunderstanding if you knew what you were talking about (as people did at that time) ... 6 * 59 = 354, less than necessary for covering a solar year. They had to add another 59 days, 354 + 59 = 413. In other words, they jumped over Roto Iri Are to arrive at Tama (the new year child). This system necessitates corrections. 413 - 365.25 = 47.75, and if there were 413 days in year 1 there could be no more than 354 days next year of course. 365.25 - 354 = 11.25 and the original discrepancy of 47.75 days would then shrink to 47.75 - 11.25 = 36.5 (strangely like a tenth of 365). Surely they must have found good methods for solving such a simple problem. Then the 6 double zodiacal constellations were divided in two to create 12 signs. A 13th odd sign, The Serpent, was added to extend the year from 354 days to 364 (= 14 * 26). It was odd, and therefore 'dark' (like a valley between mountains). Consequently it could not survive on the maps and the length of the months were once more adjusted, away from 26 to a system where 12 * 30 = 360. Later, the dark 5 days between the regular 360-day years were erased from the maps, by integrating them in a system with the pattern 31, 30, 31, 30 etc. The old system 30, 29, 30, 29 etc had returned in a somewhat modified form. The knuckles of the hands could once again be used, and we are now approaching Te Pei.
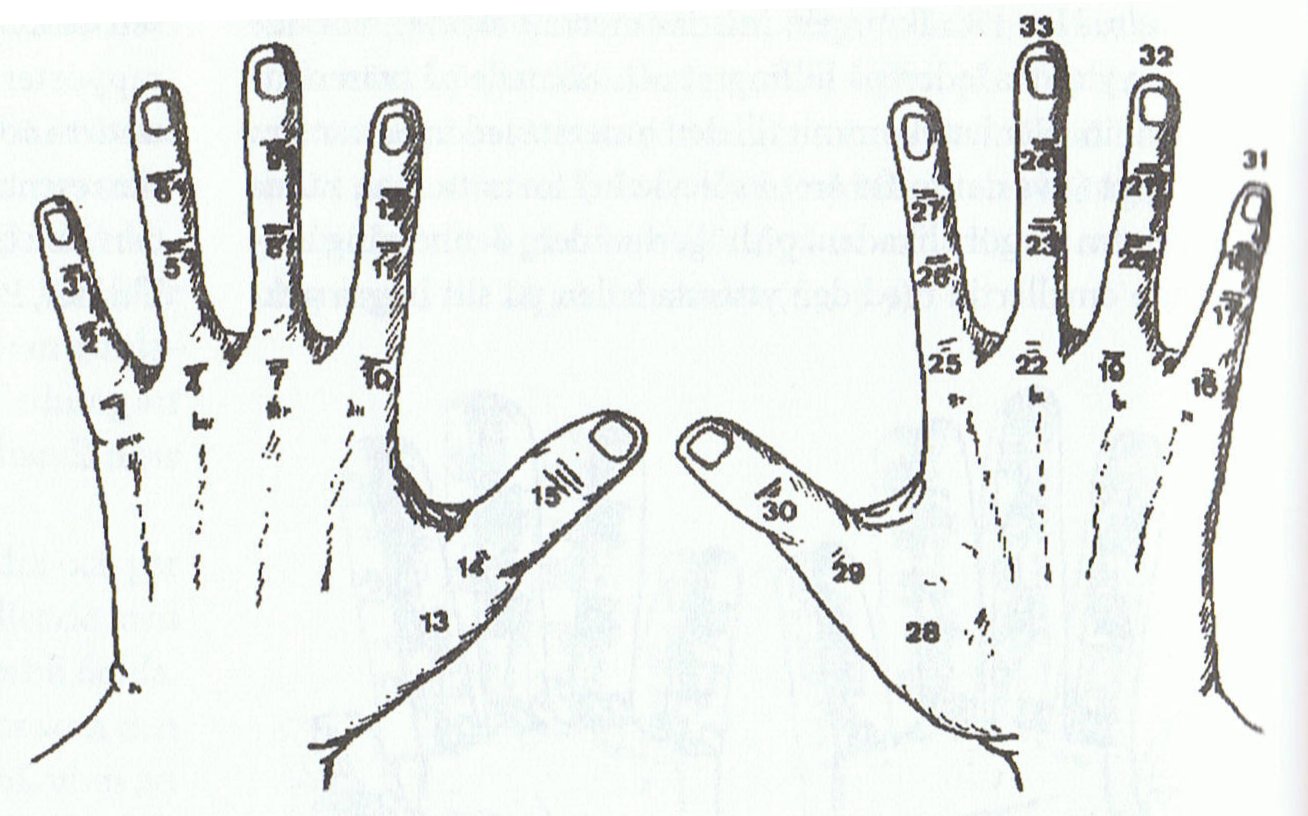
(Ifrah)
... A trace in our own calendar of the 'bicycle' idea remains. As a child I learnt the peculiar pattern of the number of days in each month by counting on the knuckles of my left hand, pointing with the index finger of my right hand. You starts with January having 31 days (represented by the knuckle corresponging to the index finger of my left hand. Then followed in the 'bay' between the knuckles of my index and long fingers February - an exceptionally 'low' dip, then March once again was 'high' on the knuckle corresponding to my left hand long finger, implying 31 days. April was 'down' (30 days) before May again was on a knuckle (31). It was very easy to remember. When June arrived 'low' it was 30 days, and July was given 31 by being located on the knuckle of my little finger. Then I had to shift and continue on my right hand, pointing with my left index finger. August (knucke of right hand index finger) was therefore also 31 days (not 30 which would follow from a more regular pattern ). It nicely explained why both July and August had 31 days, in spite of following after each other. It also - now - illustrates why right hand corresponds to sun and why a new cycle must begin after 7 months. A gap then comes, shifting from one hand to next. The gap in a way corresponds to a 'bay', because then a new knuckle comes. Shifting from one hand to the next illustrates the 8th 'hidden land' ... The structure of the moon with 4 cycles - waxing, waning, waxing, waning - during 59 nights is nicely mirrored in the fingers of the hands, the original calculator. The valleys between the fingers work equally well as the valleys between the knuckles. You need to be able to count to 4 - the thumbs have no part in the game. They are obviously of another kind. You need 3 fingers for the day and 4 when measuring the parts of the night. In K this pattern recurs in the form of multiples of 22, with a sign consisting of 14 glyphs embedded between the 1st part of the 'day' and the 2 parts arriving later:
The double-month is like the shells of a mussel, there is a hinge keeping them together. The hinge is equal, in this model, with Te Pei, the hidden 8th land. It is the valley between the hands, where the gnomon is inserted in order to continue measuring also the sea. The left hand is equal to the right hand, yet different. They are mirror images. Likewise, the road up the mountain is equal to the road going down. Sun rises towards midsummer, then declines the same way. But obviously it is a different way coming down. Autumn is different from spring. The hinge at Kb1-7 is a crucially important part. It marks the apex after a steady climb. From there 'night' on the backside of the mountain comes. From Te Pei sun moves towards west, in G illustrated by the kuhane stations on side a and ending at Nga Kope Ririva. Likewise, the text of K says Nga Kope Ririva is the last station on the map:
A short henua glyph marks when sun comes to Nga Kope Ririva. Another, longer, henua glyph marks when sun comes to Te Pou:
The two shell halves appear quite similar, yet they are qualitatively different. From Te Pei the kuhane moves eastwards along the southern coast of Easter Island, finally leaving at One Tea. In G this means reading from the beginning of side b to its end. The beginning is the hinge, Te Pei, and the end describes One Tea. The southern coast of Easter Island is no cycle, it is a linear stretch of land. After leaving at One Tea moon goes out of sight in the east and will later return at the western horizon again. It takes no more than one or two nights. It is a cycle. The boustrophedon writing on the tablets resemble the undulating paths of sun and moon. An even number of glyph lines means you will come back as in a cycle. The sinus curve is created by following a spot on the wheel moving forward. With 8 glyph lines on each side (as in G) Te Pei should be given room in the text. In K there are only 5 lines on each side. The creator of the K text must surely have deduced that the front cycle should be described. The number of glyphs can therefore be read as equal to the number of days of the front wheel. If sun leaves the island by moving towards the horizon in the west, he will be last seen at Nga Kope Ririva, at the end of the text. As a later step in creating the text, the idea must have arrived to use the text also to map the whole double cycle. Instead of thinking in terms of 8 stations on each side of the tablet, a measure of 4 quarters for each side could be used. The back side (b) should house Te Pou, as the next to best sun in the sky. 2 * 4 = 8 quarters would each have 1 glyph line. We can see why glyph lines a1 and b1 were made similar in kind, they both stand as first lines and they both have special functions. They do not belong to the 4 + 4 = 8 regular calendar. They rather both function as hinges. In G we can extrapolate backwards from the beginning of the text on side a and conclude that before Te Piringa Aniva in glyph line a1 we must have Te Pei (the hinge). The parallel text in K should likewise have Te Pei before the beginning of line a1. While Te Pei is 'beyond the horizon in the east' on side a (like the pit from which sun soon will rise), it is clearly visible on side b (the moon side). The hinge belongs to the moon. On the other hand, it is not possible to see Nga Kope Ririva with preceding kuhane stations otherwise than on side a. The Polynesians knew the world south of the equator was like the world north of the equator, with the equator connecting the worlds like a hinge, and so of course must the people on the American continent have known from very ancient times. The New World knew that there were two shells in the mussel (bivalve). Cosmos was like a moving bicycle. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


