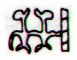|
Our symbol for eight (8) is designed as if to inform the reader that
eight consists of two equal parts, each of which has four units.
Anciently, they saw 'earth' as a 'square', i.e. a time measure
consisting of four units. The problem of 'squaring the circle' could
have meant to find the 4 points which divides the circumference of
the time cycle into 4 equal parts, for instance by counting 360 days
as 4 times 90.
With two 'years' in a year, a
similar structure would be to count 4 times 90 twice: 2 * 4 * 90 =
720. But in order to get it right, each half of the year must then be
counted against half days:
4 * 90 * ½ = 180
Similarly, to reach 180 days by
counting to 8 could have meant to count twice 4 times by using
quarter days (6 hours):
4 * 90 * 6 + 4 * 90 * 6
= 4320 hours = 180 days
Once it was important to use units
of the same kind as that which was going to be counted. They must be
in harmony with each other.
In G the kuhane stations
clearly are tuned in to number 8. The journey of the sun on side a
goes to Te Pei, a station which seems to be located at high
summer.
Eight is called varu in
Polynesian:
|
Varu
1. To cut one's hair (te puoko).
2. To shave. 3. To paint, to put on make-up: he varu
te kiea. Varu a-roto, to have diarrhoea.
Vanaga.
1. Eight. 2. To shave, to remove the
beard, to shear, to clip, to rasp, a plane. Varuvaru,
to peel, to remove the bark, to plane, to scrape, to
shear. Churchill. |
The same word (varu) is used
for a plane, i.e. a flat surface. At the solstices, where the sun is
taking a rest before returning, the terrain is level. It is natural
to count to 8 (varu) in order to reach such a place. Number
and terrain are in harmony.
|