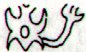Next pages:
3. The number
of sun is 6. If the Pleades are regarded as a constellation with
6 stars,
and if they announce a soon to come solstice (maybe both
solstices), then, in order for the double maitaki sign to
represent Tauono, there should be 6 'stones':
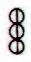 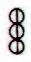
The vertical line through maitaki could
mean that each 'stone' is a double-month. A
regular solar year has 6 * 60 = 360 days.
Another
possibility is that the vertical line has at left 3 sequential
periods
and at right another sequence of 3 periods, i.e. 6 periods which are ordered by the
string rather than by the 'stones'. This possibility may have been
used in e.g. Ka4-8, where the 'stones' at left appear to be
different from those at right:
The 'stones' presumably represent two periods, but we can only
see half of each such period, represented by a semicircle. Such semicircles appear in other glyph types
too, for instance at the top respectively the back of the head in
Aa7-8 and Aa7-11:
|
5. The Pleiades
cannot be
observed at all times. Makemson says that 'thirty or
forty days' after their disappearance 'in the rays of the
setting Sun toward the end of April' the Pleiades 'are visible
on the eastern horizon just before dawn':
|
30-40 days invisible |
April/May |
Matariki i raro |
|
heliacal rising |
June |
|
start for ritual calendar |
July |
|
rising in the evening |
November |
Matariki i nika |
|
new year |
November/December |
It is not clear if also on Easter Island they defined
periods Matariki i nika and Matariki i raro by
observations in the evening, or in the early morning. In the
latter case the table above is wrong. Likewise, of course, if they did
not use the concept at all.
If they watched the Pleiades both in the morning
and in the evening, it is conceivable that they had a new year
which began according to evening observations and a ritual
calendar which began according to morning observations.
The rays from
the sun 'kills' a part of the cycle of the constellation. The stars are
there, but cannot be seen. It is very much like when the new
moon is still dark because it is in the sight line between the
observer and the sun, bathing in 'vaiora a Tane'.
Otherwise a star or constellation can be observed during half a
year (given a fixed time in the night for the observations), from its appearance in the east to its disappearance in
the west. It takes ca 2 quarters (182 days) to travel 180º.
Once there were 13 constellations
in the zodiac, but one was eliminated (the Serpent). If we count
12 / 13 of 182 days we get 168, an important number in the
rongorongo texts. Maybe the period of invisibility was
regulated to be 182 - 168 = 14 days. Twice that comes not far
from Makemson's estimate 30 - 40 days.
Another alternative would be to
stipulate 32 days' invisibility:
|
182 |
168 |
14 |
28 |
|
182 |
167 |
15 |
30 |
|
182 |
166 |
16 |
32 |
Te Pou (Sirius) is located at 9 * 29.5 = 265.5 (or rather
day number 266) and 100 days later the solar year is ending at
365.25 (or rather day number 366). The redmarked alternative
with 32 days of invisibility and 166
days of visibility is to prefer because of the harmony. And the
ancient Egyptians associated the reappearance of Sirius with new
year.
|
The qualities of 166 and 168 are different. If 182
= 14 + 168, then the moon seems to be in focus. If 182 = 16 + 166, then Sirius.
Only 182 = 15 + 167 obviously refers to the sun.
|
28 |
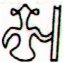 |
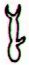 |
 |
|
Ga6-24 |
Ga6-25 (166) |
Ga6-26 (167) |
| 29 |
 |
 |
 |
|
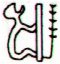
Ga6-27 (168) |
Ga6-28 |
Ga6-29 |
The figure in Ga6-28 (where 6 * 28 =
168) could refer to the invisible phase - there are no 'eyes'. The period is
number 29.
In K there is an interesting maitaki glyph
to study:
| 29 |
 |
 |
 |
 |
 |
|
Kb4-10 |
Kb4-11 |
Kb4-12 |
Kb4-13 (166) |
Kb4-14 (167) |
|
30 |
 |
 |
 |
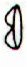 |
 |
|
Kb4-15 (168) |
Kb4-16 |
Kb4-17 |
Kb4-18 |
Kb4-19 |
Kb4-13 has a variant of the hand gesture 'waving goodbye'
(or 'handing over') connected to maitaki. Could it mean that the
season of maitaki is ending? The similar hand gesture in p.m. supports
this interpretation:
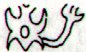 |
|
Aa1-30 |
5 + 5 = 10 glyphs distributed in
periods 29-30 should be compared with 3 + 3 = 6 glyphs in periods 28-29 in G,
and we can see the parallel Kb4-14 and Kb4-19 as the 'end of sun on the island'
respectively the 'head containing new life'. Tamaiti in Kb4-15 (and
period 30) comes in the 'new life' period, and with 168 indicating moon that is
correct - 30 is one night beyond the black number 29.
Aa1-30 is also one more than 29.
Maybe Kb4-13 is the beginning of a new season (without maitaki):
 |
50 |
 |
90 |
 |
25 |
 |
 |
22 |
|
Ka1-24 |
Ka4-8 (75) |
Kb4-13 (166) |
Kb5-20 (192) |
Ka1-1 |
|
52 |
52 |
23 |
|
192 |
If there are 2 days
for each glyph, then 91 glyphs of maitaki (from Ka4-8 to Kb4-13) will
be 182 days. And the rather meaningless 23 glyphs at the end will be a meaningful
46 days.
Possibly we should
read Kb5-15 (with ordinal number 187 and - maybe - day number 374) as a 4th and final
maitaki glyph. 5 * 15 = 75 = the ordinal number for Ka4-8 (with 4 * 8
= 32):
 |
50 |
 |
90 |
 |
20 |
 |
|
Ka1-24 |
Ka4-8 (75) |
Kb4-13 (166) |
Kb5-15 (187) |
|
52 = 4 * 13 |
22 |
|
164 = 8 * 8 + 100 |
192 will then be
equal to 8 * 8 + 100 + 28.
 |
... |
 |
 |
 |
 |
 |
 |
|
Kb5-10 |
Kb5-12 |
Kb5-13 |
Kb5-14 |
Kb5-15 |
Kb5-16 |
Kb5-17 |
|
364 |
368 |
370 |
372 |
374 |
376 |
378 |
|
182 |
184 |
185 |
186 |
187 |
188 |
189 |
Kb5-10 (with 5 * 10 = 50) will be
the end of the regular calendar, either with 1 day per glyph or with 2 days
per glyph. Then comes a non-existent glyph, maybe a glyph which never was
there, a 'black' glyph.
If the missing glyph 'carries' two
days, then its absence solves the dilemma of how to illustrate 1¼
days.
In Kb5-12 there are 2 'feathers' at
right as if to indicate that the 2nd cycle of the year now will begin. With
2 days per glyph it could mean that the year is beginning in the middle of
the K text, with 1 glyph per day it could mean that the year is beginning at
the beginning of the K text.
Kb5-14 is the last glyph in a season
with 8 'feathers', we can read. But 372 / 8 = 46.5 and 186 / 8 = 23.25,
which seems odd. Maybe there is a reference to Kb5-12 (where 368 / 8 = 46).
184 / 8 = 43 is not equally good, indeed rather bad. Therefore we presumably
should count with 2 days per glyph.
Kb5-14 can also be read as 12 * 31 =
372. In that case Kb5-15 needs a new light, with (maybe) both sun (5) and
full moon (15) present.