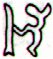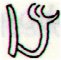The last glyph in period no. 9 is Ea4-6. Next
comes a partition with 208 glyphs (though a sum
with a question mark). These constitute 11
sequences, which together with the first 9 sum up to 20:
|
Sequence no. |
Number of glyphs |
Sequence no. |
Number of glyphs |
|
1 |
15 |
11 |
47 |
|
2 |
8 |
12 |
10 |
|
3 |
9 |
13 |
15 |
|
4 |
12 |
14 |
19 |
|
5 |
11 |
15 |
39 |
|
6 |
10 |
16 |
12 (?) |
|
7 |
11 |
17 |
7 |
|
8 |
18 |
18 |
8 |
|
9 |
12 |
19 |
8 |
|
10 |
16 |
20 |
27 |
|
Total
number of glyphs |
314 |
Here the
trouble starts. 314 emerges as the sum, but a question mark
hovers over sequence number 16. That question mark needs further
study.
314 = 7 + 99 +
208. The number of glyphs in the 1st sequence in the table above is 15, i.e.
the 7 glyphs in the 'introduction' partition are included.
7 + 99 =
106 (= 2 * 53) is a rather meaningless number, but 208 is quite
interesting, because it is equal to 8 * 26 - evidence for the 12
glyphs in sequence 16 being correct.
|
53 is a prime number, therefore I state it is rather meaningless. Small prime numbers, like 3, 5 and 7 are not meaningless, on the contrary they are immediately possible to grasp and they have qualities.
Multiples of small prime numbers maybe take on the qualities of their components. E.g. are 8 and 16 generated from 2, and they have a quality of harmony and balance.
The 16th sequence has an even number of glyphs (I believe), and so do sequences number 8 and 2.
In fact all even numbered sequences are 'tainted' by the quality of 2, except sequences number 14 (19) and 20 (27), where more powerful signs govern.
Sequences with odd numbers similarly have odd numbers of glyphs, except sequences number 9 (12) and 19 (8).
From these observations it seems obvious that there cannot be 13 glyphs in sequence number 16.
Next page:
Barthel has this
picture of line Ea8:

I have used
Fischer's pictures:
|
With 13 as the reconstructed number for period 16 in the K calendar, and from the fact of even numbered sequences in E normally have an even number of glyphs, the conclusion must be that period 16 in the K calendar has an odd number of glyphs because of its special nature. Let us investigate, though, if the periods in the K calendar follow the same pattern as the sequences in E:
|
period no. |
glyphs |
sum glyhs |
period no. |
glyphs |
sum glyhs |
|
1 |
7 |
*56 |
17 |
3 |
*55 |
|
2 |
3 |
18 |
*7 |
|
3 |
4 |
19 |
4 |
|
4 |
3 |
20 |
4 |
|
5 |
2 |
21 |
3 |
|
6 |
3 |
22 |
6 |
|
7 |
2 |
23 |
2 |
|
8 |
2 |
24 |
2 |
|
9 |
2 |
25 |
3 |
|
10 |
2 |
26 |
3 |
|
11 |
3 |
27 |
5 |
|
12 |
2 |
28 |
4 |
|
13 |
3 |
29 |
5 |
|
14 |
2 |
30 |
4 |
|
15 |
3 |
*56 + *55 = *111 |
|
16 |
*13 |
Numbers preceded by asterisks (*) are reconstructed . |
For 'higher' (>9) period numbers the pattern is there: Only 5 of the periods (16, 18, 19, 23, 26) are redmarked, meaning exceptions to the rule. 'Lower' (<10) period numbers have the opposite pattern: Only 2 of the periods (1, 8) are bluemarked.
Ea8-4 (immediately before the discussed 'vacancy') looks like the upper part of ua:
 |
 |
|
Ea8-4 |
ua |
The implication is that beyond Ea8-4 darkness arrives. In darkness you cannot see.
Next page:
My intuition
tells me to keep 12 as the number of glyphs in period 16 of E.
The condition of the Keiti tablet is, in general, very
good. Fischer:
"... a beautiful piece,
showing only a small amount of surface pitting (wormholes),
especially at the upper right-hand side of the recto. The bottom
left-hand corner was lightly chipped. The tablet was fluted."
As the tablet
was fluted its glyphs will not easily be erased. The
wormholes may have been there already when the text was
carved into the wood. I believe so.
Furthermore, our
experience with a non-existent glyph at the center (pito)
in H should be taken into consideration:
The 16th glyph
is not there. In the 16th period of K glyphs are destroyed
(or were never there in the first place). In the 16th
sequence of E a wormhole may have been used for a
non-existent glyph.
A 'worm-hole
glyph' beyond Ea8-4 would have ordinal number 261 (counted
from the beginning of side a). 261 = 9 * 29 and once again
29 pops up - 29 is the ordinal number of viri in
Ka2-5.
I think this is
evidence for not counting the 'worm-hole glyph' - glyphs
must be 'in the light' to be counted. 12 will therefore
remain my estimated number for the glyphs in sequence 16 of
E.
Counting beyond
the assumed worm-hole, to the end of the 208 glyphs, we will
reach 54 as their number. 54 = 3 * 18 is satisfactory and
314 will then be equal to 260 + 54.
|
Checking ordinal number 261 for the 'wormhole glyph' I notice how the first 7 glyph lines (Ea1-Ea7) add up to 256 = 16 * 16: