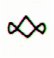At the top of Ca1-20 there is a little piece of 'string' pointing up. If we calculate with 364 'nights' for a year, and operate with 7, and deduct 180 for the sun half of the year, there will be room for 7 * 26 = 182 nights in the moon half. 180 + 182 = 362 is not reaching up to the full year measure.
Furthermore, the 'twigs' have 'knees', which makes me imagine each 'twig' as illustrating 14 + 14 = 28 nights, with waxing moon shown by the upward line and waning moon as the downward line. 7 * 28 = 196.
Then there is a pattern 2 + 2 at left of the 'midstring' and at right a pattern with 3 isolated 'twigs' with different intervals between them. Possibly 2 + 2 at left should be regarded as the 4 quarters of the sun 'year'. Moon is shining during summer too. The extra space between the 2-groups would then represent midsummer. At left means what has passed away.
In Ca1-19 the 'berries' at right are closer to the 'stem' than those at left, which presumably means that the 2nd half of the summer 'year' has sun closer to the ground - darkness awaits.
The 'midstring' in Ca1-20 should represent autumn equinox due to its location in the glyph sequence. The argument can be used for identifying the left 'twigs' with the summer 'year'.
On the other hand, given that in Ca1-19 the left 2 'berries' refer to seasons before midsummer and the right 2 'berries' to seasons after midsummer, we should imagine because of its location - after summer and at a point of vero - an interpretation of the 'berries' in Ca1-20 as reflecting the picture in Ca1-19. This implies that it is midwinter (not autumn equinox) which is illustrated by the 'midstring'. Two doublemonths, therefore, would be illustrated before midwinter and three isolated doublemonths afterwards.
4 * 28 = 112 and 3 * 28 = 84.
112 + 84 = 196.
If we add 4 (maybe the difference between 364 and 360, maybe the number of the top little string) we reach 200 ( = 10 *20).
If the dark part of the year covers 200 days, there will remain 364 - 200 = 164 days for the summer part.
164 = 4 * 41. If 364 - 360 = 4, then the pattern should repeat also for the summer 'year' - there are 4 extra days in addition to 4 * 40 = 160 days.
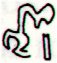
In Ca2-2 the hand has - at first glance - 4 fingers. The 3rd quarter ends at autumn equinox with the 'death' of the sun. Maybe the extra finger has been added to enable a sign of 'spooky' to show how in the last triplet (finger) of periods sun is no longer present?
 |
1st quarter | 3 + 3 |
 |
3rd quarter | 4 |
| Ca2-5 | Ca2-2 | ||||
 |
2nd quarter | 3 + 3 |
 |
4th quarter | 3 |
| Ca2-6 | Ca2-3 | ||||
| sum | 12 | sum | 7 | ||
The sum of fingers and toes measure 12 for the 1st 'year' and 7 for the 2nd 'year'. Counting only fingers we get 6 + 7 = 13.
Why are there toes during the 1st 'year' but not in the 2nd 'year'? Maybe the reason is to indicate how moon (toes) governs up to midsummer?
Counting 'kiore+henua' in Mamari we arrive at:
|
|
 |
 |
The 3 at left seems to be a separate group. | 3 | ||||
| Ca1-18 | Ca1-25 | Ca2-23 | ||||||
 |
 |
 |
 |
 |
 |
6 | 7 | 19 |
| Ca3-1 | Ca3-4 | Ca3-8 | Ca3-13 | Ca3-16 | Ca3-20 | |||
 |
Ca14-211 connects to Cb2-7 by way of contrast. | 1 | ||||||
| Ca14-211 | ||||||||
 |
 |
 |
 |
 |
 |
6 | 12 | |
| Cb2-7 | Cb2-16 | Cb2-22 | Cb3-2 | Cb3-6 | Cb3-12 | |||
 |
 |
 |
 |
 |
 |
6 | ||
| Cb3-15 | Cb3-20 | Cb4-2 | Cb4-7 | Cb4-12 | Cb4-16 | |||
 |
Cb14-11 has no henua (cfr Ca14-211 with only a short henua). | 1 | ||||||
| Cb14-11 | ||||||||
Reading the henua we find sun present on side a, moon on side b (because of the 'sucked-in' short ends).
Yet, the numbers (7 and 12) seem to tell the opposite story, i.e. sun and moon are together on both sides. However, it is an illusion:
3 * 6 = 18 and 20 * 18 = 360. We can add the blackmarked 3 + 1 + 1 to reach 365. Ca14-211 (*Ca14-17) is located at what probably signifies the 'death of the sun', and that blackmarked 1 explains the difference between 365 and 364. From this we learn the meaning of the dreaded 17, one beyond haś (16).
A single 6 refers to the sun, while twice 6 refers to the moon. 1 as long as sun is present, 2 when he has 'left' (i.e. no longer is 'right' - in front of us). When sun is at left, moon automatically takes his place. She never 'leaves' (!).
.The 'twigs' in Ca1-20 maybe are reflected in the shapes of the figures? If so, then we must study side a:
 |
 |
2 * 56 = 112 ? | 200 ? |
| Ca3-1 | Ca3-4 | ||
 |
 |
||
| Ca3-8 | Ca3-13 | ||
| the top string = 2 + 2 = 4 ? | |||
 |
A little 'feather' at
top right in the henua alluding to haś? Knee illustrating a cardinal point. |
3 * 28 = 84 ? | |
| Ca3-16 | |||
 |
Ghost status in henua. | ||
| Ca3-20 | |||
 |
Toes have left contact with henua. | ||
| *Ca14-17 | |||
Given that each 'twig' in Ca1-20 represents 28 days, which seems reasonable (note ordinal number 20 as in 200), then the sunny part of the year should have 4 quarters with 40 days in each quarter. 4 * 40 + 4 = 160 + 4 = 164 and 7 * 28 + 4 = 196 + 4 = 200.
Is this imagined structure compatible with the one in the G calendar?
We have seen that the first 3 periods in the G calendar may be special:
|
... Maybe the 4
quarters are reflected in
periods 0-3? The number of
glyphs is 26:
In Ga2-22 the old 'fish' is at left (in the past). In Ga2-28 we see the 'fish' turned upside down and from its body grows a new branch with 4 feather marks. In Ga2-29 we can read the next stage in the development of the 'fish', because the unusual (non-spooky) niu obviously is the reincarnation of the upside down fish. In Ga3-13, presumably, the 3 'spooky' limbs illustrate the same situation as in Ga2-21. In Ga3-4 'fins' hanging down at the sides may allude to the moon sickle, in which case we see the reversal of the top sign in Ga3-13, where the tu'a part is 'living' (the 3 non-spooky limbs). Upside down canoe means 'dead'. Period 2 (with manu rere marking the high point of the year) has signs of 'fruit' (hua), a characteristic of the 2nd 'year'. Also, the season has one 'sun eye' (in Ga3-7) and one 'moon sickle' (in Ga3-6), which should be compared with double 'sun eyes' (Ga3-10 and Ga3-12) and none 'moon sickle' (Ga2-10) in the 3rd period. |
Also periods 16-18 are special (only one period - 16 - in the parallel K calendar). Maybe periods 1-3 represent a spring equinox season and periods 1-18 an autumn equinox season? If so, then the proper 'summer' periods will be 4-15, i.e. 12 periods:
| G | period no. | number of glyphs | ||
|
1, 2, 3 |
8 + 4 + 7 = 19 |
35 |
19 |
|
|
4, 5, 6 |
3 + 2 + 3 = 8 |
27 |
||
|
7, 8, 9 |
4 + 2 + 2 = 8 |
35 |
||
|
10, 11, 12 |
2 + 3 + 2 = 7 |
35 |
42 |
|
|
13, 14, 15 |
4 + 3 + 5 = 12 |
54 |
||
|
16, 17, 18 |
3 + 6 + 7 = 16 |
70 |
||
| 19, 20, 21 | 5 + 8 + 5 = 18 | 30 | 88 | |
| 22, 23, 24 | 4 + 3 + 5 = 12 | 100 | ||
| 25, 26, 27 | 2 + 2 + 3 = 7 | 30 | 107 | |
| 28, 29, 30 | 3 + 3 + 4 = 10 | 117 | ||
| 31, 32, 33 | 6 + 4 + 3 = 13 | 130 | ||
| 34, 0 | 3 + 7 = 10 | 10 | 140 | |
The sum of 19 glyphs in the 'spring equinox season' and 16 in the 'autumn equinox season' is 35, a sign meaning 420 / 12.
Half of the number of glyphs in periods 1 - 18 are 'central' (blue above) and the other half 'peripheral' (red).
There are 4 blue 'quarters', in the meaning of triplets of periods, maybe the 'berries' in Ca1-19.
2 of the 3 isolated 'twigs' at right in Ca1-20 maybe correspond to the 2 redmarked triplets above. 140 - 35 = 105 = 3 * 35. Or maybe, rather, the 3rd of the 'twigs' at right in Ca1-20 represents the 2 redmarked triplets?
If we mirror the structure of the 1st half in the calendar, discovered above, we find in the 2nd half a core of 4 'droplets' (triplets of periods) in 22-33. The number of glyphs add up to 12 + 7 + 10 + 13 = 42 (a promising sign).
The rest of the 2nd half of the calendar (as structured by me above) will have 18 + 10 = 28 glyphs.
140 = 4 * 35, i.e. there are 4 lunar 'droplets' in the G calendar and they are distributed all over the year.
Period number 0 is presumably two periods, i.e. there are 18 + 18 = 36 periods all together, and of these 4 * 3 = 12 are located around the solstices, which leaves 24 = 2 * 12 periods for 'true summer' respectively 'true winter':
| 0 |
|
|
 |
 |
 |
|
|
| Ga2-20 | Ga2-21 | Ga2-22 | Ga2-23 | Ga2-24 | Ga2-25 | Ga2-26 | |
| 4 | 3 | ||||||
4 will here refer to the 4 'berries' of the sun 'year' while 3 refers to the absent sun season.
| G |
period no. |
number of glyphs |
||
|
1, 2, 3 |
8 + 4 + 7 = 19 |
35 |
19 |
|
|
4, 5, 6 |
3 + 2 + 3 = 8 |
27 |
||
|
7, 8, 9 |
4 + 2 + 2 = 8 |
35 |
||
|
10, 11, 12 |
2 + 3 + 2 = 7 |
35 |
42 |
|
|
13, 14, 15 |
4 + 3 + 5 = 12 |
54 |
||
|
16, 17, 18 |
3 + 6 + 7 = 16 |
70 |
||
|
19, 20, 21 |
5 + 8 + 5 = 18 |
30 |
88 |
|
|
22, 23, 24 |
4 + 3 + 5 = 12 |
100 |
||
|
25, 26, 27 |
2 + 2 + 3 = 7 |
30 |
107 |
|
|
28, 29, 30 |
3 + 3 + 4 = 10 |
117 |
||
|
31, 32, 33 |
6 + 4 + 3 = 13 |
130 |
||
|
34, 35, 36 |
3 + 4 + 3 = 10 |
10 |
140 |
|
The blackmarked winter solstice 6 periods add up to 29 glyphs, indicating the lunar (2) 'black cloth' (9). On the other hand, 10 and 19 refer to the sun (1).
The redmarked summer solstice 6 periods add up to 34 glyphs, i.e. the number of 'true' periods (after eliminating the two zero periods). 34 = 2 * 17.
How can we find any similarity with the 'twigs' of Ca1-20?
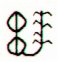
We counted with 28 for each twig, which leads us to:
| 4 * 28 = 112 and 3 * 28 = 84. 112 + 84 = 196. If we add 4 (maybe the difference between 364 and 360, maybe the number of the top little string) we reach 200 ( = 10 *20). If the dark part of the year covers 200 days, there will remain 364 - 200 = 164 days for the summer part. 164 = 4 * 41. If 364 - 360 = 4, then the pattern should repeat also for the summer 'year' - there are 4 extra days in addition to 4 * 40 = 160 days. |
Fundamentally wrong - it seems - is the difference in length between summer and winter.
We have established the possibility of 4 lunar 'droplets' covering the whole year (as interpreted from the G calendar).
364 / (4 + 3) = 52.
If each lunar 'droplet' carries 52 nights, each such 'droplet' will have 4 'mini-droplets' with 13 nights.
(13 * 4) * 7 = 364.
The summer 'year' will have (13 * 4) * 4 = 208 nights and the winter 'year' will have 364 - 208 = 156 = (13 * 4) * 3 nights. Summer is 16 * 13 and winter is 12 * 13, together 28 * 13 = 364 nights for a year.
Therefore, the 4 solar 'droplets' in Ca1-19 presumably cover only summer, and each solar 'droplet' probably corresponds to 52 nights.
We have established that Ca1-20 (with a structure reflecting that in Ca1-19) probably covers the whole year, i.e. there are 4 'twigs' in summer and 3 'twigs' in winter. Each 'twig' is divisible in 2 parts: 52 = 2 * 26.
3 stands for the moon because of its 3 phases (waxing, full, waning). Confirmation is seen in Aa1-14 and Eb6-8 (6 + 8 = 14):
 |
|
| Aa1-14 | Eb6-8 |
| marai | te kava - te rakau |
The structure arrived at has certain resemblances with that in the moon calendar of Mamari, e.g.:
| beyond autumn equinox |
 |
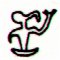 |
|
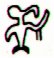 |
| Ca1-21 | Ca1-22 | Ca1-23 | Ca1-24 | |
| beyond Otua (Ca7-16) |
 |
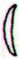 |
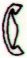 |
|
| Ca7-21 | Ca7-22 | Ca7-23 | Ca7-24 | |
| Maśre | Ina-ira | Rakau | Omotohi |
The broken henua at Omotohi corresponds to the open-ended henua at the moon elbow in Ca1-24. The same ordinal number in the line (24) and 6 lines later (a7 - a1).
3 moon sickles can be discovered in each 4-glyph sequence. In addition, in Ca1-22 a special 'moon' functions as 'boat', possibly corresponding to the one in Ca7-23 (Rakau). A ship (miro) is made of wood (miro) from a tree (rakau).
It looks as if Ca1-22 corresponds to Ca7-23 and Ca1-23 to Ca7-22. Maybe we should shift the sequence Ca1-21--24 around:
| beyond autumn equinox |
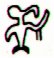 |
|
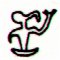 |
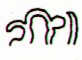 |
| Ca1-24 | Ca1-23 | Ca1-22 | Ca1-21 | |
| beyond Otua (Ca7-16) |
 |
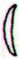 |
 |
|
| Ca7-21 | Ca7-22 | Ca7-23 | Ca7-24 | |
| Maśre | Ina-ira | Rakau | Omotohi |
Is there a 'mirror' at autumn equinox?