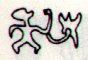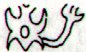TRANSLATIONS

next page previous page up home

Next page connects vae kore to hau tea:

 

A vae kore glyph is located to the right of the last of the 8 'expanding hau tea' in Tahua:

 

Aa4-63 Aa4-64 Aa4-65 Aa4-66 Aa4-67
Aa4-68 Aa4-69 Aa4-70 Aa4-71 Aa4-72

Aa4-71 is the 1st glyph beyond the predicted location of the '4th viri' (which however had been pushed away 19 positions):

100 361 17 270
Ab7-26 Ab8-43 Aa4-70 Aa4-71 Aa5-7 Aa8-26
464 = 16 * 29 290 = 10 * 29

Vae kore in Aa4-71 is therefore an integrated part of the sophisticated viri structure in Tahua, and its role is to be at the beginning of sequence of glyphs stretching up to the last ('cut off') viri (Aa8-26). But its role is even more remarkable - it also serves as glyph number 364 counted from pito in Ab8-43:

362
Ab8-43 Aa4-71
364 = 13 * 28

It is necessary to repeat the viri structure, which has been used and referred to several times earlier in the glyph dictionary. As soon will be shown, vae kore works as a kind of mirror image of viri.

The link leads to a series of pages:

A description should start by repeating how the 4 viri glyphs have been characterized by me earlier:
Ab1-1 Ab7-26 Aa5-7 Aa8-26

Ab1-1 is harmoniously drawn, but short in contrast to Ab7-26. Aa8-26 has a thick bottom 'tail' end, whereas Ab7-26 contrariwise has a thick upper 'tail'. Aa5-7 and Aa8-26 are drawn as if deformed. Neither the top part nor the bottom part in Aa5-7 is thick, and the glyph is slightly stooping forward, as if it was old. The top end in Aa8-26 looks as if it has been cut off.

Ab1-1 is located (we can infer by its short stature and other circumstances) to be the place of 'birth' and Aa8-26 to be the place of 'death'. Ab7-26 has a prominent upper part - it is located in 'high light', and from there the development proceeds downwards. Metoro began reading at the right place, at the beginning of side b:

Ab1-1 Ab1-2

Ab1-2 is number 672 counted from Aa1-1, and 672 = 4 * 168 = 24 * 28. The sunlit time is over. 28 is the number of nights in a month when sun is 'looking at' the moon, and 24 = 4 * 6, i.e. what could be called 4 'quarters of the sun'.

Ab1-1--2 together indicate the 'birth' of a season in moon light, because the crescent is drawn integrated with hau tea. The Egyptian 'ducklings', on the other hand, were drawn as entitites separate from the crescent 'nest', they are little sun birds:

Three sets of two wings is equal to six wings. Their heads are drawn similar to how sun once used to be drawn all over the world, with a black pupil. Though in the rongorongo texts such a pupil will never be seen, because the fundamental rule was to draw only outlines.

If we regard the three little birds as a.m., noon, and p.m., the diurnal season of the sun, then there are no 'quarters of the sun'. 12 / 3 = 4, i.e. if sun is 'present' during 12 hours, then each little bird will have 4 hours.

The three wives of the sun, who at the same time each 'came down' (from the pole) with a little boy (a little 'sun bird') could be three of the phases of the moon (waxing, full, and waning). The 4th phase (new moon) instead generates a new moon.

The beaks of the little birds are drawn to illustrate 3, and 3 * 3 = 9 should therefore be regarded as the time span for them. At 10 they no longer exist. 9 is the largest digit.

From appearing in Aa1-18 up to the reversed tapa mea in Aa1-27 there are 9 glyphs, a sign that the 'real sun' is 'killed' at Aa1-26.
Aa1-16 Aa1-17 Aa1-18 Aa1-19 Aa1-20 Aa1-21
Aa1-22 Aa1-23 Aa1-24 Aa1-25 Aa1-26 Aa1-27
Aa1-28 Aa1-29 Aa1-30 Aa1-31 Aa1-32 Aa1-33 Aa1-34

Similarly, 6 glyphs are used for p.m., and at Aa1-33 also the 'stand-in sun' is 'killed'. 4 * 6 = 24 'feathers' are used for a.m. and 2 * 6 = 12 for p.m., i.e. 3 sets of 12 'feathers' - one set for each 'sun boy'. Two of them are 'used up' when noon is reached. Or - alternatively - two boys arrive in the morning, but only one of them survives past noon.
Aa1-35 Aa1-36

Next page:

Next we turn to the end of the cycle:

... There are 1334 glyphs in Tahua. The text can be used as a calendar with viri glyphs marking the main divisions (in multiples of 29 glyphs) ...  the overall 'map' of the structure can be regarded as:

58 520 752
Aa8-85 Ab1-1 Ab7-26 Aa8-26
2 * 29 522 = 18 * 29 754 = 26 * 29

The beginning of the text is at Ab1-1 and the end at Aa8-85. With an even number of glyphs there are two central glyphs ...

Here we realize that in Aa8-85 the three little 'sun ducklings' still are unhatched.

Expanding the time from Ab7-26 to Aa8-26 we can see how moon is used to measure beyond the 'high light viri', because 16 refers to the number of nights defined (on Easter Island) for waxing moon:

100 361 17 270
Ab7-26 Ab8-43 Aa4-70 Aa4-71 Aa5-7 Aa8-26
464 = 16 * 29 290 = 10 * 29

Glyph number 364 (Aa4-71) has an ordinal number connected with the moon and the sun together, because the number of nights in a month when moon is 'seen' by the sun is 28 and 364 = 13 * 28.

464 is equal to 364 + 100, and 4 * 64 = 256. This is hardly a coincidence, which next page will show.

16 appears as a component of 464, and we remember how in G the kuhane stations described were 16 in number (from Maunga Hau Epa up to Poike). Moon - not sun - measures the time. In 464 we the figure 6 is initiated by 4 and succeeded by 4.

Next page:

Numbers are essential when constructing a complex calendar, and we have earlier discovered how also 1000 was used:

... If we count from Aa5-7 up to and including Ab1-1 we reach an interesting sum, viz. 1 + 272 + 1 + 59 + 1 = 334 glyphs. Between Ab1-1 and Aa5-7 there are 1000 glyphs (as if to give compensation for loosing the position at 16 * 29):

1000 272 59
Aa5-7 Aa8-26 Ab1-1
334

We will need this piece of information later on. As to 256 this number has been defined earlier and it necessary to repeat the text in extenso because it is essential for our understanding of the 'viri structure' of Tahua:

There are 3 glyphs between the last of the viri (with 'cut-off' upper 'tail') and the pair Aa8-30--31:
3 53 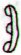520 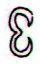752
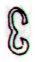Aa8-30 Aa8-31 Aa8-85 Ab1-1 Ab7-26 Aa8-26
2 * 29 522 = 18 * 29 754 = 26 * 29

Counting from Ab1-1 we will find Aa8-31 to be glyph number 1280. 521 + 754 + 5 = 1280. Aa8-31 is the 5th glyph beyond the last viri.

Counting in groups of 5 (which is the natural way to do it, using one hand to look at and the other to count with), and in the beginning being restricted to simple addition and subtraction, how do we reach such a large number as 1280?

Before true multiplication could be grasped indefinitely large numbers could be reached by doubling. 1 seed of grain on the first square of the chess board, 2 on the second, 4 on the third etc will within a short time lead to astronomically large numbers.

Fact is, the series 1, 2, 4, 8, 16, 32, 64, 128, 256 ... was used for conveniently reaching large numbers. The Mamari moon calendar has 8 periods and the 16th is the last night of growing moon. 64 is the number of squares on a chess board and 16 is also a square number - square as the earth (which moon resembles).

256 is also a square: 16 * 16 = 256. (All terms in the series 1, 2, 4, 8 etc which have odd ordinal numbers are squares.) The 'earth year' - when sun is close instead of being far away and the season is 'in the water' - ought to be 256 days (like a 'great growing moon' season). If we double the number of fingers on one hand 8 times we reach 5 * 256 = 1280.

Beginnning with 1 it is necessary with 9 'doublings' to reach 256, not 8 as I wrote. 9 is the highest digit.