|
TRANSLATIONS
Barthel had another construction with question marks: ... Arrival and departure are accompanied by intermediate stages that amount to ten days. In all, the actions of the explorers are fixed by fourteen dates, which can be arranged into seven pairs of dates. These seven pairs, whose number corresponds to the number of explorers, are made up of 35 + 5 + 5 + 5 + 5 + (corrected) 5 + 10 = 70 days or seven groups of ten days each. Half the time [of 70 days] is taken up by the sea voyage, the other half by events on land. So far it is not known what coded information is concealed in this scheme ... Let me try to explain: The sea voyage takes half the time because half the time represents the 'year'. The 'year' from autumn equinox to spring equinox is the season of the sea (consequently a sea voyage), while the other 'year' is the season of the land. By using a '7th flame' for the Sun it will reach 420 days, which is a station reached by the Moon using 15 periods (ą 28 sunlit nights). Using the perspective of the Moon it will have two 'years' ą 210 nights. We remember the Hall of the Two Truths with a double row of 21 judges of the dead: 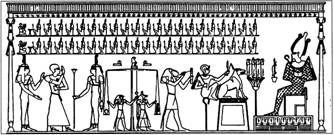 15 is the number of nights to reach full moon from new moon and 15 is the number of 28-night months needed to reach conjunction with the sun. Sun has two 'years' and so has Moon. At 210 nights there is a halfway station on the road to the conjunction with the Sun. Sun has 3 double-months in each 'year', and so has the Moon. Each of the 3 lunar double-months covers 70 nights, that is why Barthel found number 70 in manuscript E. The sea-voyage of the explorers took 35 nights, in other words ½ a lunar double-month. Another ½ maybe covered time for events on land, though I am not convinced of that. Events on land should be counted by the sun and not by the moon. The explorer's travel lasted one solar 'year' (3 double-months ą 30 days = 180 days) + the time needed for the sea voyage from Easter Island back to Hiva, i.e. 180 + 35 = 215 days in all (given that the return trip took equally long time). According to my solution the time the explorer's used for activities on land was 180 - 35 - 35 = 110 days. I have deducted another ½ lunar double-month. They stayed 'one month' at Pu Pakakina and 'one month' at the yam plantation, which leaves us with 110 - 60 = 50 solar days (or 110 - 70 = 40 lunar nights) for the rest of their activities. Though adding the red-marked days below we reach: 5 + 20 + 5 + 7 + 5 + 27 + 5 + 2 = 76, which together with 10 + 10 (= 20 black-marked) days amounts to 96 days:
From these 76 + 20 = 96 days should be drawn those 35 nights calculated for ½ a lunar double-month, which leaves us with 96 - 35 = 61 nights, not the expected 50 or 40. Lunar periods should not be used on land. They rested 7 + 5 = 12 days. If we subtract these from 96 days, we find 84. That is probably the solution. They worked twice 42 days (a period in harmony with both sun and moon). By using 'cosmic numbers' we have arrived at the same conclusion at Barthel: Haga Takaśre and Haga Hōnu are special. Maybe they are to be excluded from the quarternary system:
The 15th resting place should be due to the influence of the moon (full moon after 15 nights), while the 21st resting place equals the halfway station to 42(0). From a solar perspective we should ignore counting stations nos. 15 and 21, i.e. we reach 26 as the total period length. 2 * 12 = 24 is the fundamental length, and then we add 2 which represent next period (being the residences for the future and abdicated kings). 28 primarily refers to the nights when moon is lit up by the sun, when it is 'alive'. Full attention from the sun, however, seems to be due only on the 15th and 21st nights. In some way these 2 nights relate to the last two (Papa O Pea and Ahu Akapu) which are outside the current period. Are they generated at the two resting places (Hanga Takaśre and Hanga Hōnu)? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||