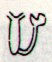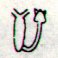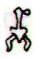TRANSLATIONS

TRANSLATIONS

In the glyph dictionary we have arrived at GD19 (hau). In Tahua we have for example Aa2-50:


Aa2-49	Aa2-50	Aa2-51	Aa2-52
ma te nuku vae	ka hahaua	ko te ariki kua noho	i te henua

We have several times earlier thought about the possible significance of Aa2-52. In Tahua ca 15 % of the henua glyphs are hatchmarked and the hatchmarks probably carry information. Some of the earlier results were:

... The glyph sequence Aa2-59--67 is a unit, because another group of glyphs is beginning with Aa2-68 and because yet another group of glyphs is ending with Aa2-58. There are 9 such groups of glyphs which seem to belong to a greater pattern, all ending similarly, viz. with hatched GD37 glyphs:


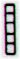
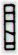
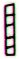
Aa2-35	Aa2-43	Aa2-48	Aa2-52	Aa2-58	Aa2-67	Aa2-77	Aa3-11	Aa3-38
5	4	4	5	4	4	6	5	4
26						15
1st half-year (?)			2nd half-year (?)			X (?)

The top short ends of the GD37 rectangles are drawn as if they were 'lopped off' in Aa2-48 and Aa3-38 (though in different directions). Presumably this means that they are 'cut short' (koti), Aa2-48 after the 1st half-year (13 hatchmarks, the last four across a very thin GD37 - midsummer) and Aa3-38 after the 2nd half-year - including the X-area - (28 hatchmarks).


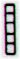
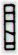
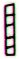
Aa2-35	Aa2-43	Aa2-48	Aa2-52	Aa2-58	Aa2-67	Aa2-77	Aa3-11	Aa3-38
1st half-year			2nd half-year			X
13			28

The pattern in Tahua maybe alloted three quadrants to the sun and one to the moon?


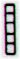
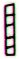
Aa2-35	Aa2-43	Aa2-48	Aa2-52	Aa2-58	Aa2-67	Aa2-77	Aa3-11	Aa3-38
1st half-year			2nd half-year			X
13			13			15

The number of hatchmarks in the X-area may indicate this. After 15 nights full moon is reached (according to my interpretation of the Mamari moon calendar). When counting double-months 15 means ¼ of the circuit of the Moon.

13 + 13 = 26 is, however, a number not divisible by 3 (to represent 3 quarters). Instead - probably - the 1st half-year is equal in length with the 2nd half-year, each being 13 * 14 = 182 nights long. A solar quarter presumably has a duration of 91 (= 7 * 13) nights. 4 of the 364 nights of the year must, though, be discarded in order to arrive at 12 * 30 = 360 nights. Then we could add a 7th solar double-month to reach 420 nights, at which point Moon will have turned around 15 times.

If we add 1 to the number of hatchmarks in the 1st half-year (representing the downward sloping top of Aa2-48) we arrive at a solar 'year' with 14 + 13 = 27 = 3 * 9 hatchmarks, which suggests 3 quarters with 90 days in each. Adding 15 (for the number of hatchmarks in the X-area) we get 27 + 15 = 42, presumably meaning 420. Adding a 7th flame of the sun (7 * 60 = 420) may be equivalent to adding the X-area. We can understand the X-area either as the 4th quarter of the solar year or as the 7th flame (or maybe even as a 'half-year' to be added - the 9 hatchmarked glyphs are divided in three groups).

7 can be understood either as the 7th flame of the sun or as the number of days in a week. Saturn, being the last day of the week, corresponds to the 7th (dark) flame of the sun. The first 6 days of the week are then corresponding to the 6 doublemonths in a solar year. 6 weeks equals 42 days and 14 + 13 + 15 = 42:


14			13			15

There is a logical lapsus in the last part - if we add 1 (representing the downwards sloping top of Aa2-48) to reach 14, then we ought to add 1 (representing the upwards sloping top of Aa3-38) also in the last group. 14 + 13 + 16 = 43. Furthermore, the double sequence 5-4-4 will be followed by 6-5-5.

Possibly, the central 13 hatchmarks - which adorn what looks like the thickest henua - represent the season when sun is present. There are no sloping tops in this group of glyphs.

The first and last groups together have 13 + 15 = 28 hatchmarks, as if to suggest the moon-lit nights in a month. The month naturally is divided into two 'seasons', waxing and waning moon. The season when sun is present ought to coincide with the third moon season - around full moon.

In Aa2-48 waxing moon is exhausted, in Aa3-38, the last phase of waning moon, there is a promise of new growth. Adding 1 in the first and last groups we have 14 + 16 = 30, which can be interpreted to include also the moonless nights.

We have now arrived at a new interpretation of the above mentioned 9 hatchmarked henua. Additional 'proof' will follow next here below.

Another way to count is to use the ordinal numbers, which we also tried earlier:

Aa2-35	Aa2-43	Aa2-48	Aa2-52	Aa2-58	Aa2-67	Aa2-77	Aa3-11	Aa3-38

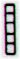
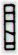
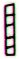
35	43	48	52	58	67	77	96	123
13			15			46

The method used here was to count the glyph distance from the 1st to the 3rd member of each group. The ordinal numbers of the nine glyphs are counted from the beginning of line a2.

Considering the ordinal numbers (counted from the beginning of line a2), it seems reasonable to associate the first group with the moon and the second with the sun, i.e. presumably with 'winter' respectively 'summer'.

35 (in Aa2-35) is half a 'lunar double-month' (35 = ½ 420 / 6), and 48 makes us remember Aa1-48 at the end of the night, and then we also realize why the órdinal number must be 43 in the middle henua:


Aa1-37	Aa1-38	Aa1-39	Aa1-40	Aa1-41	Aa1-42

Aa1-43	Aa1-44	Aa1-45	Aa1-46	Aa1-47	Aa1-48

52 (in Aa2-52) is the number of weeks in a 364 day calendar, or twice 26. While 35 was arrived at by dividing 70 by 2, here it seems reasonable to do the opposite (moon is the mirror image of the sun), viz. multiply by 2.

Aa1-52 is an example of the Rei glyph type which, we have deduced, is located at the beginning of seasons:


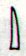
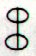
Aa1-49	Aa1-50	Aa1-51	Aa1-52	Aa1-53	Aa1

Maybe, then, 67 (in Aa2-67) is connected with Aa1-67? Maybe Aa1-67 is the last glyph in a glyph sequence?


Aa1-65	Aa1-66	Aa1-67	Aa1-68	Aa1-69	Aa1-70	Aa1-71

We have now arrived at a complex problem. On one hand - we have just discovered - there seems to be relations, governed by ordinal numbers, between the glyphs in lines Aa2 and Aa1, on the other hand we have earlier thought about the internal structure of line Aa1. Moreover, we have also found how Aa1-52 and Aa1-67 connect to parallel glyphs in H:


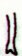
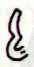
Ha6-106	Ha6-107	Ha6-108	Ha6-109	Ha6-110	Ha6-111	Ha6-112	Ha6-113
7 glyphs (Ha6-114--120)
7 glyphs (Ha6-114--120)			Ha6-121	Ha6-122	Ha6-123	Ha6-124	Ha6-125

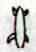Aa1-49	Aa1-50	Aa1-51	Aa1-52	Aa1-53	Aa1-54	Aa1-55	Aa1-56
7 glyphs (Aa1-57--63)
7 glyphs (Aa1-57--63)		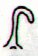	Aa1-64	Aa1-65	Aa1-66	Aa1-67	Aa1-68

These two groups of 20 glyphs have Rei as number 4 and Aa1-67 (respectively Ha6-124) as number 19. However, in H the correct division of glyphs into groups is primarily not the above. Instead we have earlier, after much work, found another group to be more important:

... The other (new) alternative is to adjust 300 to 314 to reach a symmetry with side b. Then the 20 glyphs will be Ha6-120--139:


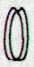Ha6-120	Ha6-121	Ha6-122	Ha6-123	Ha6-124	Ha6-125	Ha6-126	Ha6-127
7 glyphs (Ha6-128--134)
7 glyphs (Ha6-128--134)			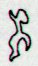Ha6-135	Ha6-136	Ha6-137	Ha6-138	Ha6-139

Ha6-120 and Ha6-139 clearly define 18 glyphs between them ...

... The new alternative of locating the 20 glyphs (on side a of H), with reconstructed numbers, is:


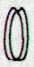Ha6-120	Ha6-121	Ha6-122	Ha6-123	Ha6-124	Ha6-125	Ha6-126	Ha6-127
*Ha6-45	*Ha6-46	*Ha6-47	*Ha6-48	*Ha6-49	*Ha6-50	*Ha6-51	*Ha6-52
*320	*321	*322	*323	*324	*325	*326	*327
7 glyphs (Ha6-128--134)
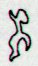			Ha6-135	Ha6-136	Ha6-137	Ha6-138	Ha6-139
			*Ha6-60	*Ha6-61	*Ha6-62	*Ha6-63	*Ha6-64
			*335	*336	*337	*338	*339

Ha6-124, with reconstructed glyph number *Ha6-49 (one more than 48) has the reconstructed ordinal number *324. When the clock strikes 24 it is a new day.