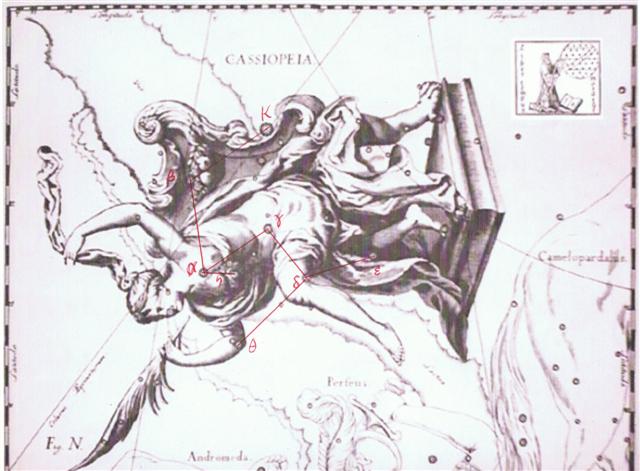
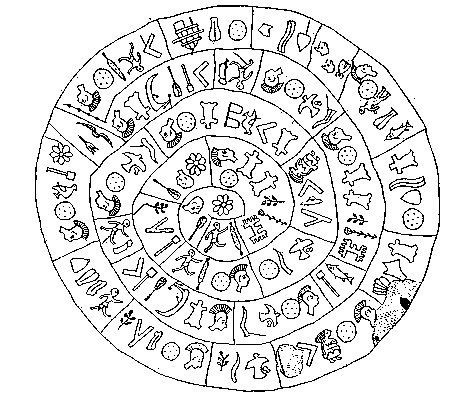
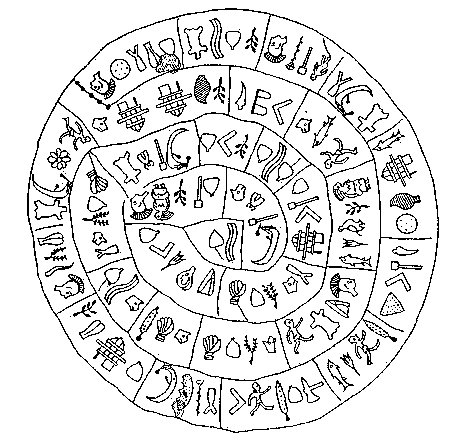
7-3. Yesterday evening I saw a description (by way of TV) of how Linear B had been deciphered. Here it was mentioned that the disc of Phaistos on Crete had 46 different types of signs ('letters') and that the disc was inscribed with 242 such signs. This struck me as no coincidence but as a way of documenting the significance of these numbers. I recalled that I early on had some reflections of my own. But at that time I was not aware of what 46 and 242 might signify. Nowadays, on the other hand, I would immediately recall the connection between 21h and 24h as a first possible association for 46: ... Allen has documented all his star culminations at 21h, which could be due to an effort of keeping the culminations at their proper places according to the ancients, 24h (spring equinox) - 21h = 3h = 24h / 8 = 45º. 3h corresponds to 366 / 8 = 45.75 of my right ascension days and *366 - *46 = *320 (Dramasa, σ Octantis) ... And as to 242 it first of all could imply 2 * 121 (→ May 1). Then 242 could also point at right ascension day *242:
On Hawaii they thought the Pleiades should ideally return to visibility in November 18 (322 - 80 = *242). ... The correspondence between the winter solstice and the kali'i rite of the Makahiki is arrived at as follows: ideally, the second ceremony of 'breaking the coconut', when the priests assemble at the temple to spot the rising of the Pleiades, coincides with the full moon (Hua tapu) of the twelfth lunar month (Welehu). In the latter eighteenth century, the Pleiades appear at sunset on 18 November. Ten days later (28 November), the Lono effigy sets off on its circuit, which lasts twenty-three days, thus bringing the god back for the climactic battle with the king on 21 December, the solstice (= Hawaiian 16 Makali'i). The correspondence is 'ideal' and only rarely achieved, since it depends on the coincidence of the full moon and the crepuscular rising of the Pleiades ... It would be strange if the number of glyphs on side b of the G tablet (242) and the number of signs on the Phaistos disc (242) were completerly unrelated to the place of the Breast of Cassiopeia (α, Schedir), culminating in the night of November 18.
I had earlier not used much effort to count the number of 'letters' on the Phaistos disc and instead concentrated on the number of divisions of the sequences of signs, presumably (I cannot remember everything) believing these signs were letters in some ancient alphabet and that the divisions marked where one word was ending and another word was beginning. Now I have to work again in order to find out if indeed there were 242 signs on the disc. Let's begin with 'side a'. Here the center has a 'sun flower' with 8 petals:
Moving withershins I will here document the number of partitions together with their number of signs:
If the TV statement 242 is correct, then we can expect side b to have 242 - 123 = 119 signs.
My question mark refers to how to interpret the string not joined at the top. If it is regarded as a 'letter', then indeed the sum 123 + 119 (?) becomes 242. If not we will have 2 * 118 + 5 = 236 + 5 = 241 ≠ 242. And if the sum on side b indeed should be regarded as 119, then we consequently ought to reduce the number of departments from 30 to 29, because my initial (19, 4) and (20, 4) will unite into (19, 9). 31 (side a) + 29 (side b) = 60 departments of signs. Another and similar problem is the prolongation of the spiral arm which on side a defines a maximum depth of 5 sequences of 'letters' and which ends in limbo so to say. We can see 4 knots where it ends. ... Among the Nahyssan of S. Carolina time was measured and a rude chronology arranged by means of strings of leather with knots of various colour, like the Peruvian quipos. The Dakota use a circle as the symbol of time, a smaller one for a year and a larger one for a longer period: the circles are arranged in rows, thus: OOO or O-O-O. The Pima of Arizona make use of a tally. The year-mark is a deep notch across the stick ... On side b the corresponding spiral arm also defines a maximum depth of 5 sequences. 5 + 5 = 10. But here the corresponding knots (drawn more firmly) are 5 in number. 4 + 5 = 9. The central place on side b has a pair of signs, and I guess we could equally well end at this place as beginning there:
61 → 366 / 6, and the impression is a description from the very top up in the sky in the north down to the lowest place south of the equator. The equator itself would then be represented by the place where the reader moves from side a of the disc to the other (side b). The total number of 'letters' now becomes 242 even without counting the string not joined at the top to the spiral arm on side b. Counting also the string not joined at the top (in department 43) will change the sum to 242 + 1 = 243. This number could reasonably represent 9 months each carrying 27 right ascension days.. 128 → 2 * 64 = 123 (side a) + 5 (department 32), and 242 (department 61) → 2 * 121 → twice 11 * 11 (as in May 1). The distance from 0h to the First Point of Aries equals 27 right ascension days and so does the distance from Bharani (*41) to Aldebaran (*68): |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||