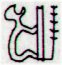
The great takaure in Gb3-1 has a position similar to that of glyph 236 - such could be suggested by the numbers - and the Gregorian day number at the only takaure on side a, for 'August 17 (229), is also suggestive of a connection with the beginning of side b:
But instead of this great takaure being at the end of line b2 (with number 2-36) it has been positioned as first glyph in line b3. August 17 is day 229 in the Gregorian calendar and day 229 at takaure in Ga4-2 implies we ought to be able to find day 365 by moving 136 glyphs ahead. 229 + 136 = 365. The glyph number at 'December 31 is 222 (= 86 + 136):
Alternatively we could find day 365 in the Gregorian calendar by moving 229 glyphs backwards, but then we have to add 107 glyphs in order to compensate for the difference between 472 glyphs and 365 days. 222 + 107 + 229 = 558 = 472 + 86. 229 - 86 = 143 ('May 23 at Gb8-30 as number 472) and 143 + 107 = 250, which is a promising number (equal to one more than the distance in days from equinox to the heliacal rising of Antares at the time of G). We are thus looking for glyph number 472 - 250 = 222 (one week before day 236 in the manzil system).
The twins in Ga8-25 have a dark henua in front (marked with a dot), possibly referring to the time of shadows north of the equator. There are 292 days from equinox to 'January 7 and Gb3-1 is glyph number 292 from Gb8-30. Nine weeks separate takaure in Gb3-1 from the twins in Ga8-25 (just like nine weeks are separating the beginning of the front side of the text from Rogo in Gb6-26). From takaure in Ga4-2 to takaure in Gb3-1 there are 435 - 229 = 206 days (= 355 - 149). Right ascension day 355 alludes to December 21. However, 'March 21 (80 or 445) does not arrive at Gb3-1 but 10 days later:
The manzil day number (309) is 100 less than the glyph number at Rogo in Gb6-26 (409), which in turn is 10 more than the synodical cycle of Jupiter. Beyond the end of this right ascension cycle comes a moe signifying a new season. But I will continue with the right ascension positions of the stars in order to complete my attempt at arranging stars in parallel with the glyphs on the G tablet. Although Caph, Sirrah, etc appear also in line b6. From Gb3-11 to Rogo in Gb6-26 there are 409 - 302 = 107 glyphs (= 472 - 365). The manzil structure continues to 'May 16 and to the heliacal rising of the Pleiades (8 weeks beyond Gb6-26):
The glyphs below appear to be quite different from those following Rogo in Gb6-26:
13 * 29½ = 383½ and this fact may have forced the creator of the G text to turn hau tea in Gb4-1 backwards and to put a droplet at front in the preceding hoea. 12 * 29½ = 354 is at the glyph preceding the great takaure:
The last star on my list is Kerb (τ Pegasi): ... The name Salm (for τ Pegasi, Kerb) is also the name of the eldest son of king Fereydun, another name of which was Apam Napat ('Son of Waters'): Salm is a character in the Persian epic Shahnameh. He is the oldest son of [the] legendary hero and king Fereydun. It is believed that his name was given to him by his father, after Salm chooses to seek safety and run instead of fighting the dragon that had attacked him and his brothers (the dragon was Fereydun himself who had disguised himself to test his sons) ... When Fereydun decides to divide his kingdom among his sons, he gives Salm [the timid unmanly one] Anatolia and West [the female side of the kingdom] ... Fereydūn ... [is] also called Apam Napat, 'Son of the Waters' ... ... τ, 4.5, with ν, was Al Sufi's Sa'd al Na'amah, which Knobel thinks should be Al Na'āim, the Cross-bars over a well; but they also were known as Al Karab, the Bucket-rope. The usual titles for τ - Markab and Sagma or Salma - are from Bayer, but the last two should be Salm, a Leathern Bucket.  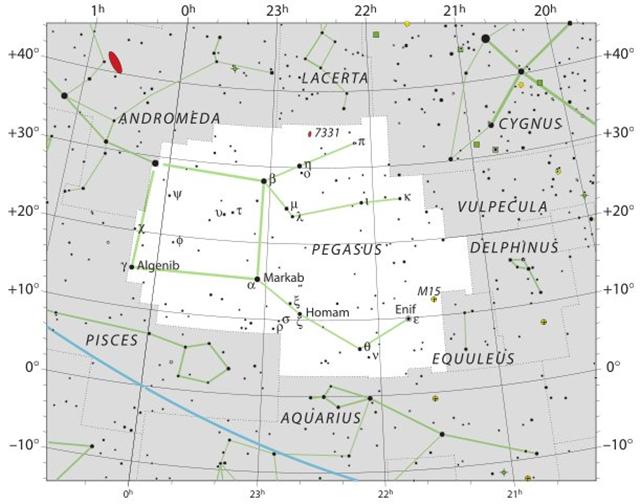 |