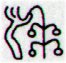
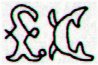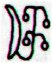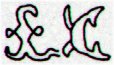Once again, the glyphs from the beginning of line Ga8:
Beyond haú at RA 272 (= 2 * 136) = Gregorian day 348 could possibly come another group of 16 glyphs:
... Wind winnowing is an agricultural method developed by ancient cultures for separating grain from chaff. It is also used to remove weevils or other pests from stored grain. Threshing, the separation of grain or seeds from the husks and straw, is the step in the chaff-removal process that comes before winnowing ...
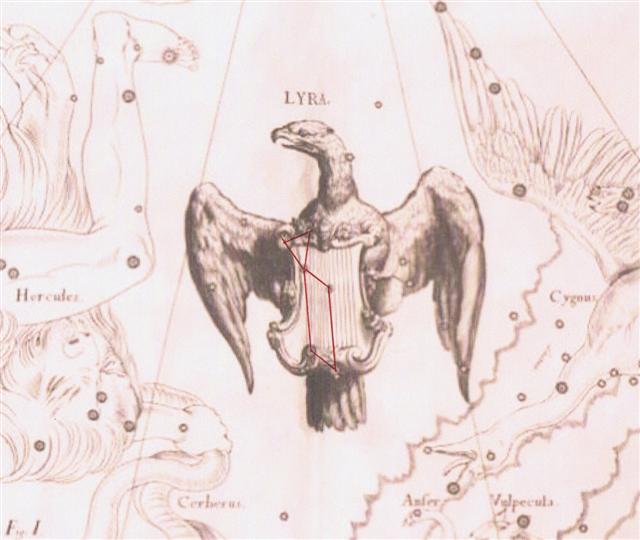
Notably Ga8-21 was at the end of Land (Nunki). The headless hanau figure in Ga8-18 coincided with the night when Atlas culminated at midnight. RA day 285 = calendar day 80 + 285 = 365 = December 31 at the time of rongorongo. Another 'coincidence'. The exceptional 22nd (as in π) Hindu station Abhijit was ruled not only by the bright (0.03) Vega but also by Double Double (ε) - a name which could mean 4 (as the normal number of hua poporo) - and by ζ Lyrae:
Therefore I guess the powerfully drawn 'schemset' (companion) curve at the top in Ga8-15 could allude to Vega. The great bird high up in the sky roof was at a point of turning around and he had no future:
Vega was a star at the pole, but at the nakshatra side of the sky compared to Thuban and Polaris:
In order not to be drowned by too much information at a time I have waited until now with presenting the heliacal dates:
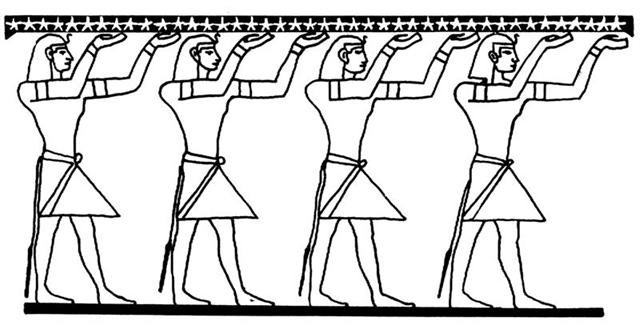
At Tua Haro 1, where the new year was beginning for those who had adjusted their time correctly, we can see a great tagata figure at left - probably representing the old year. Gregory XIII apparently changed the structure of time by moving spring equinox from March 25 (84) to March 21 (80). Therefore he could not adjust for all the differences between the Julian calendar and the effects of the true precession: ... When Julius Caesar established his calendar in 45 BC he set March 25 as the spring equinox. Since a Julian year (365.25 days) is slightly longer than an actual year the calendar drifted with respect to the equinox, such that the equinox was occurring on about 21 March in AD 300 and by AD 1500 it had reached 11 March. This drift induced Pope Gregory XIII to create a modern Gregorian calendar. The Pope wanted to restore the edicts concerning the date of Easter of the Council of Nicaea of AD 325. (Incidentally, the date of Easter itself is fixed by an approximation of lunar cycles used in the Hebraic calendar, but according to the historian Bede the English name 'Easter' comes from a pagan celebration by the Germanic tribes of the vernal - spring - equinox.) So the shift in the date of the equinox that occurred between the 4th and the 16th centuries was annulled with the Gregorian calendar, but nothing was done for the first four centuries of the Julian calendar. The days of 29 February of the years AD 100, AD 200, AD 300, and the day created by the irregular application of leap years between the assassination of Caesar and the decree of Augustus re-arranging the calendar in AD 8, remained in effect. This moved the equinox four days earlier than in Caesar's time ... The Pope may have had decided to eliminate the 4 ('double-double') raisers of the sky roof, the Bacabs. He was no pagan:
... 'Among the multitude of gods worshipped by these people were four whom they called by the name Bacab. These were, they say, four brothers placed by God when he created the world at its four corners to sustain the heavens lest they fall.' (Diego De Landa according to Graham Hancock in his Fingerprints of the Gods.) 'In the ms. Ritual of the Bacabs, the cantul kuob [the suffix '-ob' indicates plural], cantul bacabob, the four gods, the four bacabs, occur constantly in the incantations, with the four colors, four directions, and their various names and offices.' (William Gates, An Outline Dictionary of Maya Glyphs.) '... This connects up the present section with the beginning of the 'sacred tonalamatl', at the Spring equinox with the Mayas as with the Mexicans, and in the center of the 364-day year (52 days of which preceded and 52 followed the tonalamatl or tzolkin), ruled by its 91-day quarters by the Four Bacabs, whose quarternary repetition (in the 1820-day period) we have thus verified ...' (Gates, a.a.) ... On February 9 the Chorti Ah K'in, 'diviners', begin the agricultural year. Both the 260-day cycle and the solar year are used in setting dates for religious and agricultural ceremonies, especially when those rituals fall at the same time in both calendars. The ceremony begins when the diviners go to a sacred spring where they choose five stones with the proper shape and color. These stones will mark the five positions of the sacred cosmogram created by the ritual. When the stones are brought back to the ceremonial house, two diviners start the ritual by placing the stones on a table in a careful pattern that reproduces the schematic of the universe. At the same time, helpers under the table replace last year's diagram with the new one. They believe that by placing the cosmic diagram under the base of God at the center of the world they demonstrate that God dominates the universe. The priests place the stones in a very particular order. First the stone that corresponds to the sun in the eastern, sunrise position of summer solstice is set down; then the stone corresponding to the western, sunset position of the same solstice. This is followed by stones representing the western, sunset position of the winter solstice, then its eastern, sunrise position. Together these four stones form a square. They sit at the four corners of the square just as we saw in the Creation story from the Classic period and in the Popol Vuh. Finally, the center stone is placed to form the ancient five-point sign modern researchers called the quincunx ... Later on in this series of rituals, the Chorti go through a ceremony they call raising the sky. This ritual takes place at midnight on the twenty-fifth of April and continues each night until the rains arrive. In this ceremony two diviners and their wives sit on benches so that they occupy the corner positions of the cosmic square. They take their seats in the same order as the stones were placed, with the men on the eastern side and the women on the west. The ritual actions of sitting down and lifting upward are done with great precision and care, because they are directly related to the actions done by the gods at Creation. The people represent the gods of the four corners and the clouds that cover the earth. As they rise from their seats, they metaphorically lift the sky. If their lifting motion is uneven, the rains will be irregular and harmful. (Maya Cosmos)
If Hotu Matua, the 'Full Moon' king, arrived in Tagaroa Uri 15 (288), then this date may have been understood as day 288 - 80 = 208 (= 13 * 16) counted from the Hyades gate, which would be at haú and Gregorian day 348 (= 288 - 4 + 64). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||