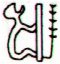
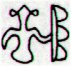In the G text there are 49 glyphs from viri in Ga5-11 to viri in Ga7-1. There were 49 days from the equinox (265) to Ko Ruti 10 (314):
Glyph 1 in line Ga7 maybe was meant to be understood as an allusion to 71, i.e. how to translate 1 precessional day into human years:
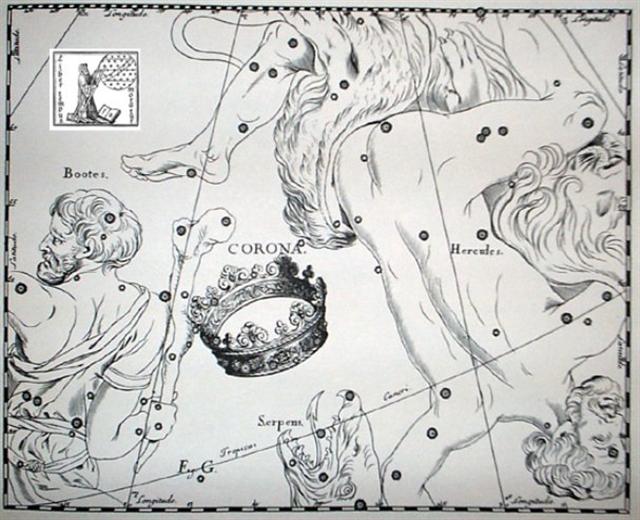
... The story of Rip Van Winkle is set in the years before and after the American Revolutionary War. Rip Van Winkle, a villager of Dutch descent, lives in a nice village at the foot of New York's Catskill Mountains. An amiable man whose home and farm suffer from his lazy neglect, he is loved by all but his wife. One autumn day he escapes his nagging wife by wandering up the mountains. After encountering strangely dressed men, rumored to be the ghosts of Henry Hudson's crew, who are playing nine-pins, and after drinking some of their liquor, he settles down under a shady tree and falls asleep. He wakes up twenty years later and returns to his village. He finds out that his wife is dead and his close friends have died in a war or gone somewhere else. He immediately gets into trouble when he hails himself a loyal subject of King George III, not knowing that in the meantime the American Revolution has taken place. An old local recognizes him, however, and Rip's now grown daughter eventually puts him up ... 49 (= 7 * 7) days could be a measure of a time in autumn outside the ordinary calendar. 229 (number of glyphs on side a of the tablet) - 49 = 180. With 7 pebbles thrown at each of 3 pillars per day, it is hard to find a simple equation with 49 on one side and 21 at the other side: ... At Muzdalifah, pilgrims collect pebbles (49, because seven are thrown at each of the three pillars each day) which will be thrown in the Stoning of the Devil ritual in Mina during the next 3 or 4 days. Pilgrims then spend the night at Muzdalifah, often sleeping in the open air, before leaving for Mina the next morning ... 49 / 21 = 7 / 3. Possibly the 3 pillars were standing there in order to 'personify' the last 3 quarters of the previous year. 7 could then allude to the 7 sleepers: ... The story is a close adaptation of Peter Klaus the Goatherd by J.C.C. Nachtigal, which is a shorter story set in a German village. The story is also similar to the ancient Jewish story about Honi M'agel who falls asleep after asking a man why he is planting a carob tree which traditionally takes 70 years to mature, making it virtually impossible to ever benefit from the tree's fruit. After this exchange, he falls asleep on the ground and is miraculously covered by a rock and remains out of sight for 70 years. When he awakens, he finds a fully mature tree and that he has a grandson. When nobody believes that he is Honi, he prays to God and God takes him from this world. Note also that the family name of Honi is also a term of geometry (M'agel is Hebrew for 'circle maker'), as well as the family name of Rip (Winkel is German for 'angle'). The story is also similar to a 3rd century AD Chinese tale of Ranka, as retold in Lionel Giles in A Gallery of Chinese Immortals. In Orkney there is a similar and ancient folklore tale linked to the Burial mound of Salt Knowe adjacent to the Ring of Brodgar. A drunken fiddler on his way home hears music from the mound. He finds a way in and finds the trowes (Trolls) having a party. He stays and plays for two hours, then makes his way home to Stenness, where he discovers fifty years have passed. The Orkney Rangers believe this may be one source for Washington Irving's tale, because his father was an Orcadian from the island of Shapinsay, and would almost certainly have often told his son the tale. The original story was by Diogenes Laertius, an Epicurean philosopher circa early half third century, in his book On the Lives, Opinions, and Sayings of Famous Philosophers. The story is in Chapter ten in his section on the Seven Sages, who were the precursors to the first philosophers. The sage was Epimenides. Apparently Epimenides went to sleep in a cave for fifty-seven years. But unfortunately, 'he became old in as many days as he had slept years'. Although according to the different sources that Diogenes relates, Epimenides lived to be one hundred and fifty-seven years, two hundred and ninety-nine years, or one hundred and fifty-four years. A similar story is told of the Seven Sleepers of Ephesus, Christian saints who fall asleep in a cave while avoiding Roman persecution, and awake more than a century later to find that Christianity has become the religion of the Empire ... In G these 49 'pebbles' are possible to explain as the difference between the ancient star calendar and the September equinox in rongorongo times: ... The pair of viri are drawn exactly alike which should mean they ought to be the same. The point of the September equinox according to Sun time appeared to come 170 - 121 = 49 days later than according to Moon time. However, 49 - 27 (the precessional depth of Al Sharatain) = 22 = 'October 14 (287) - 265 (September equinox in rongorongo times) is a better measure. In the times of Al Sharatain the star Nusakan (β Corona Borealis, at the dark inside of the Crown and close to the Club of Bootes according to Hevelius), rose with the Sun 22 days after the quinox.
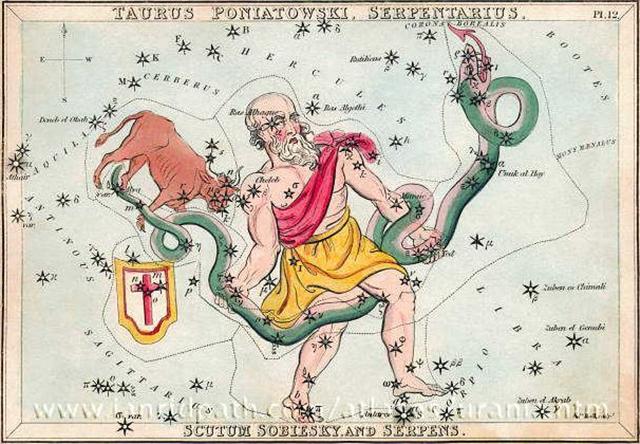
This was hardly a coincidence. When the First Point of Aries was at 0h, then 22 days beyond the equinox at the other side of the sky there was a Sign alluding to 314 (π): ... About Carmenta we know from the historian Dionysus Periergetis that she gave orcales to Hercules and lived to the age of 110 years. 110 was a canonical number, the ideal age which every Egyptian wished to reach and the age at which, for example, the patriarch Joseph died. The 110 years were made up of twenty-two Etruscan lustra of five years each; and 110 years composed the 'cycle' taken over from the Etruscans by the Romans. At the end of each cycle they corrected irregularities in the solar calendar by intercalation and held Secular Games. The secret sense of 22 - sacred numbers were never chosen haphazardly - is that it is the measure of the circumference of the circle when the diameter is 7. This proportion, now known as pi, is no longer a religious secret; and is used today only as a rule-of-thumb formula, the real mathematical value of pi being a decimal figure which nobody has yet been able work out because it goes on without ever ending, as 22 / 7 does, in a neat recurring sequence [3.142857-142857- ...]. Seven lustra add up to thirty-five years, and thirty-five at Rome was the age at which a man was held to reach his prime and might be elected Consul. (The same age was fixed upon by a Classically-minded Convention as the earliest at which an American might be elected President of the United States.) ... From the mathematical π (314 as in Ko Ruti 10) to π Corona Borealis there were 314 (ºNovember 10) - ºNovember 6 (310) = 4 days:
At the same time was also Cor Serpentis (α at the Neck of the Serpent, Unuk Al Hay):
Which makes me think of the beginning of Appendix 34 in Hamlet's Mill: "Actually, we are up against a completely incomprehensible narrative of events which occurred during a sea voyage. The plant, according to Albright (AJSL 36, p. 281, n. 2) literally 'thorny grapevine' is supposed to grow in the apsu, and to be accessible by way of a 'water-pipe'. This pipe, rātu, however, is a conjecture right here: the word occurs only later when, after his bath in a well, and the following loss of the plant, Gilgamesh complains bitterly about his frustration, i.e., about having obtained a boon for the 'earth lion' instead of for himself. The 'earth lion', identified with the thievish serpent, is assumed in its turn to live 'in a well which communicated with the apsu' (Albright, 35, p. 194). It is then (GE 11.298) that the hero says: 'When I opened the water-pipe and (...) the gear, I found that which has been placed as a sign for me: I shall withdraw and leave the boat on the shore' (Speiser trans., ANET, pp. 96f.) ..." A serpent was often used as the picture for a river. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||