The complications on side b of the tablet are presumably not absolutely necessary to discuss when reading side a. From the heliacal stars at the time of rongorongo (Rogo-Rogo) the approximate dates are anyhow possible to deduce. This was what I once did for Antares and Aldebaran:
The corresponding dates in Babylonian times (at the time of the Hyades Gate) should then have been around 64 days earlier. I have used the structure of our own Gregorian calendar for easier understanding what season for instance MARCH 22 referred to, when Ain (ε Tauri) rose with the Sun - with CAPITAL LETTERS in order to underline the necessary connections between the stars and the dates at the time of the Hyades Gate. Precession moved the Sun earlier and earlier for each generation of men, but the stars were there for ever and could still be used for finding the seasons.
The poor and lifeless state of the glyphs around the solstice could allude to how old Sun appeared to have problems with moving ahead. In contrast the beautiful little Rei which follows could indicate how south of the equator late June was not the season for the arrival of high summer but instead where the dark oppressive forces of the old year were about to be pushed down.
The stars could support such ideas, because anciently the Twins were beginning to rise with the Sun. But to understand such things it was necessary to go back to early times, foremost to the Golden Age when the Twin halves of the year climbed up on dry land on the far bank of the Milky River after the equinox had been crossed over. ... In Hindu legend there was a mother goddess called Aditi, who had seven offspring. She is called 'Mother of the Gods'. Aditi, whose name means 'free, unbounded, infinity' was assigned in the ancient lists of constellations as the regent of the asterism Punarvasu. Punarvasu is dual in form and means 'The Doublegood Pair'. The singular form of this noun is used to refer to the star Pollux. It is not difficult to surmise that the other member of the Doublegood Pair was Castor. Then the constellation Punarvasu is quite equivalent to our Gemini, the Twins. In far antiquity (5800 B.C.) the spring equinoctial point was predicted by the heliacal rising of the Twins (see fig. 6.6). By 4700 B.C. the equinox lay squarely in Gemini (fig. 6.7). 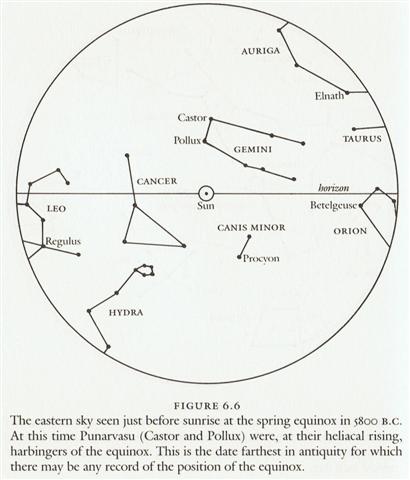  Punarvasu is one of the twenty-seven (or twenty-eight) zodiacal constellations in the Indian system of Nakshatras. In each of the Nakshatras there is a 'yoga', a key star that marks a station taken by the moon in its monthly (twenty-seven- or twenty-eight-day course) through the stars. (The sidereal period of the moon, twenty-seven days and a fraction, should be distinguished from the synodic, or phase-shift period of 29.5 days, which is the ultimate antecedent of our month.) In ancient times the priest-astronomers (Brahmans) determined the recurrence of the solstices and equinoxes by the use of the gnomon. Later they developed the Nakshatra system of star reference to determine the recurrence of the seasons, much as the Greeks used the heliacal rising of some star for the same purpose. An example of the operation of the Nakshatra system in antiquity can be seen in figure 6.9. 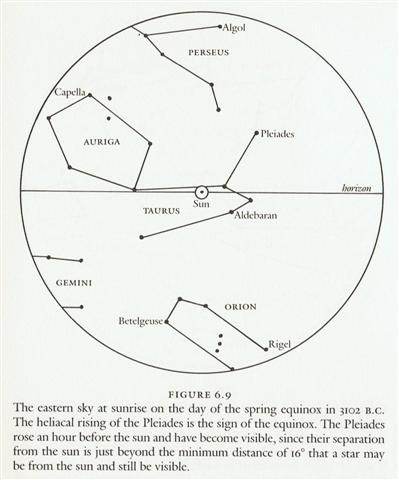 Here we see that the spring equinox occurred when the sun was at its closest approach to the star Aldebaran (called Rohini by the Hindus) in our constellation Taurus. But, of course, the phenomenon would not have been visible because the star is too close to the sun for observation. The astronomers would have known, however, that the equinoctial point was at Aldebaran by observing the full moon falling near the expected date or near a point in the sky exactly opposite Aldebaran (since the full moon is 180º from the sun), that is, near the star Antares ... The system of Nakshatras, then, is quite distinct from systems that use the appearance of heliacally rising or setting stars as the equinoctial marker. Furthermore, the Indian system is all but unique in that two calendar systems competed with each other - a civil system, in which the year's beginning was at the winter solstice, and a sacrificial year, which begins at the spring equinox. The beginning of the former was determined by the Nakshatra method, observing the winter full moon's apparition near the point of the summer solstice in the sky (as explained above). The arrival of the beginning of the sacrificial year might be determined by the Nakshatra method - observation of the spring full moon near to the autumn Nakshatra in Virgo. More commonly, however, it was determined as in the Greek system, by direct observation of the heliacal rising of a sign star. In the current calendar, for example - one unchanged since the fifth century A.D. - the yoga star of the Nakshatra Ashvini (beta Arietis) ushers in the spring equinox at its heliacal rising ... I think we can assume the creator of the G tablet used heliacal Wezen (δ Canis Major) as a time indicator, because in rongorongo times this star rose with the Sun in July 6 = 107 days after 0h (and 26 days after June 10):
The generating force of the figure in Gb6-25 - where we can suspect an allusion to day 14 * 25 = 350 = 200 + 150 = 8 * 25 (side a) + 6 * 25 (side b) - worked on (ki roto ki) the Rogo figure (14 * 26 = 364) and the result was Gemini. 14 * 27 = 378 (cycle of Saturn) and 14 * 28 = 392 (glyphs on side a of the C tablet). 392 - 4 * 14 = 336 (December 3). 471 glyphs on the tablet could have covered not only 364 days in the calendar for the Sun year but also 107 precessional days from the age when Wezen was at 0h and Gemini would have arrived immediately after the equinox (*MARCH 25 with asterisk to denote a date from the idealized birth of the system):
Mago in Ga2-14 (where 214 = 2 * 107) could via the form of the Scorpion indicate the beginning of a new half year at July 7. ... The month, which takes its name from Juppiter the oak-god, begins on June 10th and ends of July 7th. Midway comes St. John's Day, June 24th, the day on which the oak-king was sacrificially burned alive. The Celtic year was divided into two halves with the second half beginning in July, apparently after a seven-day wake, or funeral feast, in the oak-king's honour ...
January 12 is day 377 counted from January 1 in the previous year. By looking at the Full Moon in January 12 it would have been possible to find Procyon in the interval between Castor and Pollux. At the time of the Hyades Gate NOVEMBER 10 was a π day. At the time of Wezen it was day 270. ... According to the later writers Censorinus and Macrobius, the ideal intercalary cycle consisted of ordinary years of 355 days alternating with intercalary years, alternately 377 and 378 days long. On this system, the average Roman year would have had 366¼ days over four years, giving it an average drift of one day per year relative to any solstice or equinox ... In practice, intercalations did not occur systematically ... but were determined by the Pontifices ... They usually occurred every second or third year, but were sometimes omitted for much longer, and occasionally occurred in two consecutive years. If managed correctly this system could have allowed the Roman year to stay roughly aligned to a tropical year. However, since the Pontifices were often politicians, and because a Roman magistrate's term of office corresponded with a calendar year, this power was prone to abuse: a Pontifex could lengthen a year in which he or one of his political allies was in office, or refuse to lengthen one in which his opponents were in power. If too many intercalations were omitted, as happened after the Second Punic War and during the Civil Wars, the calendar would drift out of alignment with the tropical year. Moreover, because intercalations were often determined quite late, the average Roman citizen often did not know the date, particularly if he were some distance from the city. For these reasons, the last years of the pre-Julian calendar were later known as 'years of confusion'. The problems became particularly acute during the years of Julius Caesar's pontificate before the reform, 63 - 46 BC, when there were only five intercalary months (instead of eight), none of which were during the five Roman years before 46 BC. Caesar's reform was intended to solve this problem permanently, by creating a calendar that remained aligned to the sun without any human intervention. This proved useful very soon after the new calendar came into effect. Varro used it in 37 BC to fix calendar dates for the start of the four seasons, which would have been impossible only 8 years earlier ... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||