However, such important events as equinoxes and solstices ought to be updated in a calendar, because they move over time, do not stay at specific stars. Possibly this could explain the pair of ihe tau glyphs in Cb8-13 / Cb8-15:
| 'Sept 19 |
20 |
21 (264) |
'Equinox |
23 |
24 |
| 'March 20 |
'Equinox |
22 (81) |
23 |
24 |
25 (450) |
| Oct 16 |
17 (290) |
18 |
19 |
20 |
21 |
| April 16 |
17 |
18 |
19 |
20 |
21 (111) |
 |
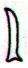 |
 |
 |
 |
 |
| Cb8-12 |
Cb8-13 |
Cb8-14 |
Cb8-15 |
Cb8-16 |
Cb8-17 (580) |
| Te ariki |
hokohuki |
te inoino |
te hokohuki |
te inoino |
te vai noho |
| no star listed (209) |
Muphrid (210.1), ζ Centauri (210.3) |
φ Centauri (211.0), υ¹ Centauri (211.1), υ² Centauri (211.8), τ Virginis (211.9) |
Agena (212.1), θ Apodis (212.5), Thuban (212.8) |
14h (213.1) |
Neck-2 |
| χ Centauri (213.0), Menkent (213.1) |
Asellus Tertius, κ VIRGINIS, 14 Bootis (214.8) |
| POLARIS, Baten Kaitos (26.6), Metallah (26.9) |
Al Sharatain-1 / Ashvini-1 / Bond-16 |
ι Arietis (28.0), λ Arietis (28.2) |
Alrisha, χ Phoenicis (29.2), Alamak (29.7) |
2h (30.4) |
η Arietis (31.9) |
| Segin, Mesarthim, ψ Phoenicis (27.2), SHERATAN, φ Phoenicis (27.4) |
κ Arietis (30.3), Hamal (30.5)
Alkes
|
Ihe means a point and tau could mean a star (or season). But I have so far not been able to understand what Metoro meant by hokohuki.
How should the end of the years be treated? In rongorongo times Cb14-1 was located 355 days after March 21 and the extraordinary pair of glyphs at March 11-12 appear to describe rather the situation in rongorongo times than in the times of Al Sharatain.
| 141 |
'February 12 |
13 (44) |
14 |
| 'August 14 (226) |
15 |
| March 11 |
12 (71) |
| September 10 |
11 (254) |
 |
 |
| Cb14-1 (722) |
Cb14-2 |
| Kua pu ia |
tatagata ariga erua |
| no star listed (355) |
no star listed (356) |
| ο¹ Centauri (173.8) |
ξ Hydrae (174.3), ο² Centauri, λ Centauri (174.8) |
A year of the old Roman type with 355 days could have been in the mind of the creator of the text. March 11 was 70 + 366 - 355 = 81 days after the December solstice (just as March 22 was 81 days after January 1). And 354 = 12 * 29½.
However, 'February 12 (43) + 366 = 409 could point at 0h because glyph 409 in G is a Rogo which probably was located at March 21.
Maybe both line Ca14 and line Cb14 were special.
| 14 |
'February 28 |
29 |
'March 1 (61) |
| 'August 30 |
31 |
'September 1 (244) |
| March 27 |
28 |
29 (88) |
| September 26 |
27 |
28 (271) |
 |
 |
 |
| Cb14-17 |
Cb14-18 |
Cb14-19 (740) |
| kokoti hia te henua |
tagata hakaitiiti |
i te henua |
| λ Phoenicis (6.3), β Tucanae (6.4) |
no star listed (7) |
DELTA (8.4), Schedir (8.6), μ Phoenicis (8.9) |
| γ Muscae (189.0), Avis Satyra (189.3), Asterion (189.5), Kraz (189.7)
Alderamin
|
α Muscae (190.2), τ Centauri (190.5), χ Virginis (190.7) |
Al Áwwā'-11 |
| ρ Virginis (191.4), PORRIMA, γ Centauri (191.5) |
My old (Al Sharatain) calendar dates suggested so far are Gregorian (or Julian), whereas 'September 12 (255) - at heliacal Spica and Alcor - could point at December 21 (355) = 100 days later as the end of the year:
Counted from vero in Cb8-6 to the end of side b there are 740 - 568 = 172 glyphs (probably days). Day 172 in the Gregorian (or Julian) calendar is June 21 (the northern midsummer).
Maybe we should use the old Roman calendar? As I have understood it this year began with the month Martius (March):
| Martius - Sextilis |
180 |
| + September - December |
118 |
| = Martius - December |
298 |
| + Ianuarius |
29 |
| = Martius - Ianuarius |
327 |
| + Februarius |
23 |
| 5 |
| = Normal year |
350 + 5 = 355 |
| + Mensis Intercalaris |
22 |
| = Leap year |
372 + 5 = 377 |
| Martius |
31 |
31 |
- |
| Aprilis |
29 |
30 |
+1 |
| Maius |
31 |
31 |
- |
| Iunius |
29 |
30 |
+1 |
| Quintilis |
31 |
31 |
- |
| Sextilis |
29 |
31 |
+2 |
| Sum |
180 |
184 |
+4 |
| September |
29 |
30 |
+1 |
| October |
31 |
31 |
- |
| November |
29 |
30 |
+1 |
| December |
29 |
31 |
+2 |
| Sum |
118 |
122 |
+4 |
| Ianuarius |
29 |
31 |
+2 |
| Februarius |
28 |
28 |
- |
| Sum |
57 |
59 |
+2 |
| Total |
355 |
365 |
+10 |
But March 1 was the first day before the Kalends of March:
... The leap day was introduced as part of the Julian reform. The day following the Terminalia (February 23) was doubled, forming the 'bis sextum - literally 'double sixth', since February 24 was 'the sixth day before the Kalends of March' using Roman inclusive counting (March 1 was the 'first day').
Below I have therefore adjusted my earlier number for days in the month Martius from 31 to 30, which leads to day number 320 at the extraordinary Cb13-10 (where we according to Metoro should count) because 297 (Martius - Sextilis) + 23 (Ianiarius 1-23) = 320:
| 306 |
'January 21 |
22 |
23 |
24 |
| 'Ianuarius 21 |
22 |
23 (320) |
24 |
| February 17 |
18 |
19 (50) |
20 |
| Februarius 17 |
18 |
19 |
20 |
 |
 |
 |
 |
| Cb13-8 |
Cb13-9 (700) |
Cb13-10 |
Cb13-11 |
| te moa |
kua vero |
te mamahia |
te vero |
| η Piscis Austrini (333.4) |
Rooftop-12 |
ι Pegasi (335.0), Alnair (335.1), μ Piscis Austrini, υ Piscis Austrini (335.3), Woo (335.7), Baham, τ Piscis Austrini (335.8) |
ζ Cephei (336.2), λ Cephei (336.3), -/270 Lac. (336.7), λ Piscis Austrini (336.8) |
| 22h (334.8) |
| Kae Uh (334.0), Al Kurhah (334.4), SADALMELIK (334.6), ι Aquarii, ν Pegasi (334.7) |
I have simplified above and not tried to show also the nakshatra dates. But, as we should remember, the other King Star (Regulus) was at RA day 152.7 = calendar day 80 + 152 = 232 (August 20), and 232 - 183 = 49 (February 18) was its nakshatra date. The distance between them did not change over time, it was in principle eternal, whereas 22h was dependent on where the March equinox for the moment was among the stars.
We can guess the creator of the C text had arranged it so that this important cardinal point - where one King was reflected by the other - was at glyph 700. But to be more exact Sadalmelik should be located a little later than at 334.6 in order to be precisely at the other side of the sky compared to Regulus. 152.7 + 365¼ / 2 = 335.3, i.e. at Cb13-10.
|
Regulus |
182 |
Sadalmelik |
183 |
|
152.7 |
334.6 |
Let's now complete our review of the last part of side b:
| 'January 25 |
26 |
27 |
| 'Ianuarius 25 |
26 |
27 (324) |
| February 21 |
22 |
23 (54) |
| Februarius 21 |
22 |
23 (Terminalia) |
 |
 |
 |
| Cb13-12 |
Cb13-13 |
Cb13-14 |
| te ariki |
te vage Rei |
te hokohuki i te inoino |
| ε Cephei (337.2), 1/325 Lac. (337.3), Ancha (337.4), α Tucanae (337.9) |
Al Sa'ad al Ahbiyah-23 / Shatabisha-25 |
β/172 Lac. (339.2), 4/1100 Lac. (339.4), π Aquarii (339.5) |
| ρ Aquarii (338.2), 2/365 Lac. (338.5), SADACHBIA (338.6) |
| 'January 28 |
29 |
30 |
| 'Ianuarius 28 |
29 (326) |
'Februarius 1 |
| BISSEXTUM (6) |
5 |
| Februarius 24 |
Februarius 24 |
25 (56) |
| δ Tucanae (340.1), ρ Cephei (340.2), ζ Aquarii (340.4), Alrediph (340.5), 5/1100 Lac (340.7), σ Aquarii, 6/650 Lac. (340.9) |
Leap night |
α/91 Lac. (341.1), Homan, β Piscis Austrini (341.2), ν Tucanae (341.5), υ Aquarii (341.9) |
| February 24 |
25 (56) |
26 |
 |
 |
 |
| Cb13-15 (314) |
Cb13-16 |
Cb13-17 (708) |
| kua moe ki te marama |
e marama erua |
te kava - te moa |
| δ Tucanae (340.1), ρ Cephei (340.2), ζ Aquarii (340.4), Alrediph (340.5), 5/1100 Lac (340.7), σ Aquarii, 6/650 Lac. (340.9) |
α/91 Lac. (341.1), Homan, β Piscis Austrini (341.2), ν Tucanae (341.5), υ Aquarii (341.9) |
η Aquarii (342.1), Situla (342.7) |
| 'January 31 |
'February 1 |
2 (33) |
3 (400) |
28 |
| 'Februarius 2 |
3 |
4 (330) |
5 |
| 4 |
3 |
2 |
1 |
| Februarius 26 |
27 |
28 (60) |
Martius 1 (60) |
| η Aquarii (342.1), Situla (342.7) |
ε Piscis Austrini (343.5), ο Pegasi (343.8) |
Matar (344.2) |
λ Pegasi (345.0), ξ Pegasi (345.1), τ Aquarii (345.7), μ Pegasi (345.9) |
| February 27 |
28 (59) |
29 (425) |
March 1 (60) |
 |
 |
 |
 |
| Cb13-18 |
Cb13-19 |
Cb13-20 |
Cb13-21 (320) |
| ihe tara tu |
te hokohuki |
te henua |
te hokohuki hoi haatu ia - te hokohuki |
| ε Piscis Austrini (343.5), ο Pegasi (343.8) |
Matar (344.2) |
Leap night |
λ Pegasi (345.0), ξ Pegasi (345.1), τ Aquarii (345.7), μ Pegasi (345.9) |
I find these results quite encouraging. Although disturbingly complicated.
In rongorongo times March 1 (60) would have been at glyph 320 counted from Cb1-1, and at Cb13-21 we could count 13 * 21 = 273 (= 3 * 91), alluding to the last day of September and the end of the winter half of the year on Easter Island.
The 'Octopus tentacles' could have measured 40 days (320 / 8 = 40) and in the times of Al Sharatain Cb13-21 was at day 400 counted from 0h in the previous year. 'February 3 = 34 + 366 = 400. But according to the old Roman calendar this was 'Februarius 5 (331), because 355 - 331 = 24 days remained of the year. 'Februarius 5 + 24 Þ 23 days to 'Februarius 28 + 'Martius 1.
11 days earlier, at day 320, was 'Ianiarius 23, precisely half a year later than heliacal Regulus.
Glyph 314 counted from Cb1-1 is Cb13-15 where in rongorongo times Bissextum would have begun, if the Julian leap day system had been used.
Side b could have had 'March 1 as its last glyph because this was the situation in the times of Al Sharatain (if not the old Roman calendar was used). At that time the Sun would have been at Delta:
| 'March 1 |
Delta |
δ Andromedae |
8.4 |
March 29 (88) |
- |
- |
| |
| 0 |
- |
Zero |
η Andromedae |
11.4 |
April 1 (91) |
- |
0 |
| 1 |
Al Sharatain |
Pair of Signs |
β Arietis (Sheratan), γ (Mesarthim) |
27.4 |
April 17 (107) |
16 |
16 |
| |
|
Musca Borealis |
35 (Head of the Fly), 39 (Kaffaljidhma), and 41 Arietis (Bharani) |
41.4 |
May 1 (121) |
14 |
30 |
| 2 |
Al Dabarān |
Follower |
α Tauri (Aldebaran), θ¹, θ²´, γ (Hyadum I), δ (Hyadum II), ε (Ain) |
63.4 |
May 23 (143) |
22 |
52 |
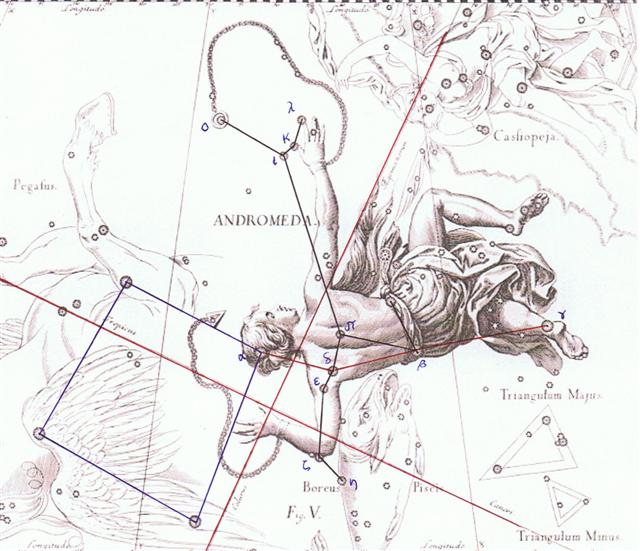
Alamak (γ), which in rongorongo times was at 29.7 would have been Andromeda's last star also in the times of Al Sharatain. It would have risen with the Sun only a pair of days after 0h.
29.7 - 27 + 183 = 185.7 = 265.7 - 80, which means Alamak would have been close to the Full Moon in September 22 (265). Stars should be watched in the night, not when they are close to the Sun.
|













