Another type of 'turtle' - a Rogo type - has the central position at the very end of side a:
| April 11 |
12 (468) |
13 |
| October 12 (285) |
13 |
14 |
 |
 |
 |
| *Ca14-24 |
*Ca14-25 |
*Ca14-26 |
| te henua |
te honu kau |
manu kake rua |
| no star listed |
Achernar (23.3) |
no star listed |
| Heze (205.0) |
ε Centauri (206.3) |
no star listed |
| April 14 |
15 |
16 (472) |
| October 15 |
16 |
17 (290) |
 |
 |
 |
| *Ca14-27 |
*Ca14-28 |
*Ca14-29 (392) |
| te henua |
te honu |
te rima |
| no star listed |
POLARIS, Baten Kaitos (26.6), Metallah (26.9) |
Al Sharatain-1 / Ashvini-1 / Bond-16 |
| Segin, Mesarthim, ψ Phoenicis (27.2), SHERATAN, φ Phoenicis (27.4) |
| τ Bootis (208.2), Benetnash (208.5), ν Centauri (208.7), μ Centauri, υ Bootis (208.8) |
no star listed |
Muphrid (210.1), ζ Centauri (210.3) |
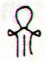
392 - 27 = 365 and an 'open hand' could show how the cycle has ended - nothing remains:
| April 16 |
17 (107) |
363 |
April 15 |
16 (472) |
| October 16 |
17 (290) |
October 15 |
16 (655) |
 |
 |
 |
 |
| Ca1-26 |
Ca2-1 (27) |
*Ca14-28 |
*Ca14-29 (392) |
| kua moe ki te tai. |
Te heke |
te honu |
te rima |
| POLARIS, Baten Kaitos (26.6), Metallah (26.9) |
Al Sharatain-1 / Ashvini-1 / Bond-16 |
no star listed |
POLARIS, Baten Kaitos (26.6), Metallah (26.9) |
| Segin, Mesarthim, ψ Phoenicis (27.2), SHERATAN, φ Phoenicis (27.4) |
| no star listed (209) |
Muphrid (210.1), ζ Centauri (210.3) |
τ Bootis (208.2), Benetnash (208.5), ν Centauri (208.7), μ Centauri, υ Bootis (208.8) |
no star listed (209) |
| 366 |
The number of glyphs from Ca2-1 to the end of line Ca14 is probably 366, which agrees with my suggestion that the year had to be counted as 366 days because there remained ¼ of a day after 365 days had been counted.
Counting a year ahead from Polaris (26.6 + 365¼ = 391.82) should, it appears, result in a position at *Ca14-28. However, if the year was a leap year, then the position ought to be at April 16. In a leap year the correlation between the Gregorian dates and the RA dates are upgraded with the adjustement by February 29:
| leap year |
April 16 (107) |
RA 26 |
| ordinary year 1 |
April 16 (106) |
RA 26+¼ |
| ordinary year 2 |
April 16 (106) |
RA 26+½ |
| ordinary year 3 |
April 16 (106) |
RA 26+¾ |
| leap year |
April 16 (107) |
RA 26 |
| etc |
In order to simplify matters I have everywhere assumed April 16 corresponds to RA day 26, i.e. in my presentations the Gregorian day numbers for an ordinary year are to be translated into RA day numbers by simply subtracting 80. In the interval from the nakshatra date October 17 at Ca2-1 to the last glyph on side a there would also be a February 29 which correspondingly changed the nakshatra stars (and dates) ahead with 1 step.
|