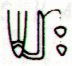If we assume there was a calendar year ending with
80 days from January 3 up to and including May 23:
|
Shaula 1 |
2 |
3 |
4 (600) |
5 (236) |
|
January 3 |
4 |
5 |
6 (736) |
7 (372) |
 |
 |
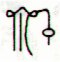
 |
 |
 |
|
Ca11-4 |
Ca11-5 |
Ca11-6 (290) |
Ca11-7 |
Ca11-8 |
 |
 |
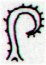 |
 |
 |
|
Ga8-21 |
Ga8-22 |
Ga8-23 |
Ga8-24 |
Ga8-25 (*292) |
|
73 |
Saad Al
Saud 12 |
13 (311) |
|
March 22
(81) |
23 |
 |
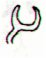 |
|
Ca1-1 |
Ca1-2 |
 |
 |
|
Gb3-12 |
Gb3-13 |
then February 9 will correspond to its day
number 365 + 40 - 2 = 403:
|
Al
Baldaah 12 |
13 |
|
February 9 (40) |
10 |
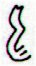 |
 |
|
Ca12-9 (325) |
Ca12-10 |
403 was also the RA day of Sirius, we
remember:
 |
 |
 |
 |
|
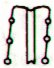
Gb6-17 |
Gb6-18 |
Gb6-19 |
Gb6-20 (403) |
|
no star listed |
ν Puppis (99.2), ψ3 Aurigae (99.4),
ψ2 Aurigae (99.5) |
ψ4 Aurigae (100.5), |
Sirius (101.2),
ψ5 Aurigae (101.4) |
|
June 27 (178) |
28 |
29 |
30 |
|
Al Tuwaibe' 2 (42) |
3 |
4 |
5 |
80 + 101 = 181 (June 30) and 403 (Gb6-20) +
63 = 466 = 365 + 101. By the way, glyph 466 (Gb8-24) corresponds to
Sheratan 1 (May 17) and there is therefore a similarity
between June 30 and May 17:
 |
 |
|
 |
 |
|
Gb8-22 |
Gb8-23 |
Gb8-24 (466) |
Gb8-25 |
|
Atiks, Rana (55.1), Celaeno, Electra,
Taygeta (55.3) |
Maia, Asterope, Merope (55.6), Alcyone
(56.1), Pleione, Atlas (56.3) |
no star listed |
Menkhib (57.6) |
|
May 15 |
16 (136) |
17 |
18 |
|
14 |
Alrescha 15 (365) |
Sheratan 1 |
2 |
February 9 is day 325 counted from March
21, 40 + 365 - 80 = 325, and once Julius Ceasar decided
March 25 (3-25) was the date of spring equinox. In
Ca12-10 the Sun is high in front and in Ca12-12 the Sun
is also in front, though possibly past his best date:
|
Al Baldaah 12 |
13 (270) |
|
February 9 (40) |
10 |
 |
 |
|
Ca12-9 (325) |
Ca12-10 |
|
oho te vae |
ki hukiga
o te ra |
|
Saad Al Thabib 1 |
2 (272) |
|
February 11 |
12 |
 |
 |
|
Ca12-11 |
Ca12-12 |
|
kua oho ra |
kua ere te tagata - te
hetu |
Al Baldaah 13 is manzil day 270. In the
Gregorian calendar day 270 is September 27. In my
assumed C calendar day 270 corresponds to September 29.
The words of Metoro can be interpreted
to first state what (or who) is leaving (oho).
The 80 nights long season was possibly regarded as a season
of leaving the old 'Land' behind.
Maybe the upright (huki) at left in
Ca12-10 'causes' (o) the Sun (te ra) - a
new 'Land' - to rise:
| Huki
1. Pole attached to the poop
from which the fishing-net is
suspended: huki kupega. 2. Digging
stick. 3. To set vertically, to
stand (vt.). 4. Huki á te mahina,
said of the new moon when both its horns
have become visible. Vanaga.
1. To post up, to publish.
2. To cut the throat (uki). Mq.:
Small sticks which close up the ridge of a
house. Ha.: hui, the small uniting
sticks in a thatched house. Churchill.
Standing upright. Barthel.
M. Spit for roasting.
Te Huki, a constellation. Makemson.
Hukihuki. 1. Colic.
2. To transpierce, a pricking. 3. To sink to
the bottom. Churchill. |
|
O
Ó;
1. Prepositon marking the genitive. 2.
Preposition expressing the cause, the
reason: because of (also i):
e-tahataha-á te vaka o te tokerau. the
boat rocks from side to side because of the
wind. 3. Lest, in order not to... e-ûi
koe o higa, be careful not to fall. 4.
Sometimes used as conditional: if, whether;
ina kai agiagi au o tu'u-mai te Matu'a,
I don't know if the Padre has arrived.
5. Article sometimes used preceding proper
names; ó Hotu Matu'a, ó Santiago. 6.
To answer saying 'oh'; ana ragi te tagata
ki te rua tagata, 'hé koe?', he-ó-mai,
he-kî: 'ó, î au', when a man calls
another, asking 'where are you?' (the other)
answers saying 'oh, I am here'. O; to
celebrate a festival: he-o i te gogoro.
Vanaga.
1. Tai o, rippling
water. (Compare in some sea sense - Mgv.:
akao, a narrow arm of the sea, to throw
stones into the water in order to drive fish
into a net.) 2. Of. Mgv., Mq., Ta.: o,
of. 3. A verb sign; o mua, at first;
ina o nei, to be away
(not-being-here). Churchill. |
|
Raa
Sun; day; i te raá nei,
today; raá îka, good day for fishing.
Vanaga.
1. Sun. 2. Day. 3. Time.
4. Name of sub-tribe. Fischer.
Te manu i te raá
= comet.
Barthel.
'... The substitution of the
sun for the sail, both of which are called
ra or raa in Polynesia, is a
remarkable feature in Easter Island art ...
' Heyerdahl 3.
1. The sun;
raa ea mai,
raa puneki,
sunrise; raa
tini,
raa toa,
noon. P Mgv., Ta.:
ra,
the sun. Mq.:
a, id. 2. Day, date;
a raa nei a,
to-day, now;
raa i mua, day before. P Mgv.,
Ta.: ra,
a day. Mq.:
a, id. Churchill.
'... The chief thus makes his appearance at
Lakeba from the sea, as a stranger to
the land. Disembarking at the capital
village of Tubou, he is led first to
the chiefly house (vale levu) and
next day to the central ceremonial ground (raaraa)
of the island ...' (Islands of History)
Ta.:
toraaraa,
to raise up. Churchill 2. |
What constellation was together with
Sun in early February and what constellation could
be seen with Moon in the night? What constellation
was Te Huki?
|
Al Baldaah 12 |
13 (270) |
Saad Al Thabib 1 |
2 (272) |
|
February 9 |
10 |
11 |
12 |
 |
 |
 |
 |
|
Ca12-9 (325) |
Ca12-10 |
Ca12-11 |
Ca12-12 |
|
oho te
vae |
ki
hukiga o te ra |
kua oho ra |
kua ere te tagata - te
hetu |
|
Yan (324.6) |
Alphirk (325.7),
Sadalsud (325.9) |
Castra (327.2),
Bunda (327.5) |
Nashira (328.0) |
|
ω Leonis (142.6), τ¹ Hydrae (142.7), ψ
Velorum (143.3), Alterf, τ² Hydrae
(143.4), ξ Leonis (143.5) |
A Hydrae (144.1) |
Ukdah (145.4),
κ Hydrae (145.5) |
Subra (145.8), ψ Leonis (146.4) |
|
August 11 |
12 |
13 |
14 (226) |
|
Murzim 8 |
9 |
10 |
11 (90) |
It is not obvious what my answer
should be. On one hand a Knot (Ukdah) is
necessary when a fishing-net has to be
attatched to an upright, on the other hand I
have suggested the images on one side of the sky
are reflected at the other end of the sky, which
means there should be some kind of 'mirror knots' around RA day
327 (February 11).
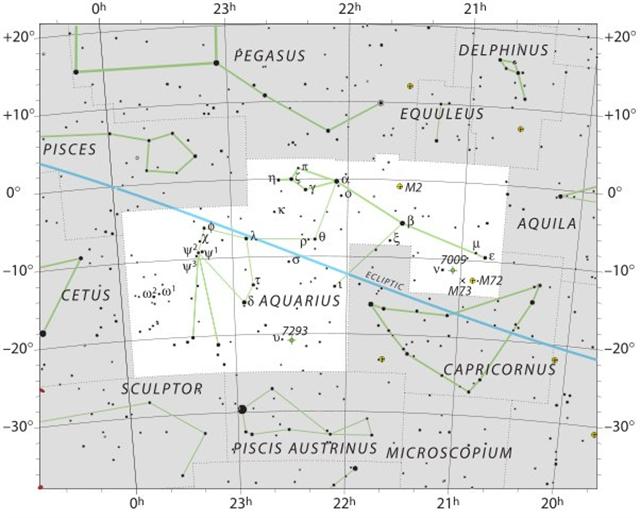
Sadalsud is
β Aquarii
and Bunda is ξ. Maybe the Capricorn outline was
imagined as a boat from which a net was suspended.
Te Huki could then have been the succession
of stars beginning with ε (Albali) and
stretching to κ (Situla), measuring out 423
(February 27) - 394 (January 29) = 29 days:
|
Al Baldaah 2 (259) |
|
January 30 (395) |
 |
|
Ca11-31 (315) |
|
te inoino |
|
σ Pavonis (314.7),
Albali (314.8) |
|
August 1 (213) |
|
Alhena 11 (77) |
|
no star listed |
Situla (κ
Aquarii) was at RA day 343 = February 27
(58 = 343 + 80 - 365):
|