The distance from Aldebaran to Antares was less than the distance from Antares to Aldebaran, which agreed with the fact that the northern summer was slightly shorter than the southern summer - the orbit of the Earth around the Sun was not a perfect circle. Over time the fixed stars were not so fixed, they moved slowly against the background with different speeds and in different directions. By investigating this as regards the distance from Aldebaran to Antares I found out that around 5000 B.C. the distance would have been around 177 days, i.e. equal to 6 lunar synodic cycles. 6 * 29 ½ = 177.
... In 3000 B.C. Aldebaran would have risen heliacally in March 21 and (3000 + 1842) / 26000 * 365¼ = 68.0, where I have guessed 1842 A.D. was the year which served as a point of reference for the rongorongo writers. And their conventional number of years for a complete precessional cycle could have been 26000 years. I have used the length of the year according to the Julian calendar - 365¼ days and slightly longer than the correct estimate - for calculating how many years were necessary in order to measure out 1 precessional day: 26000 / 365¼ = ca 71 years and (3000 + 1842) / 71 = ca 68 days ... But the names Ana-mua (Anatares) and Ana-muri (Aldebaran) meant they belonged together and therefore the distance to consider was rather 182 days than 181 days. In which case the rest of the year would become 183 days:
I.e., unless the observer was south of the equator, where summer was longer and the distance from Antares up to and including Aldebaran could be counted as 183 + 2 = 185 days. Or as the situation would have been in 3000 B.C. when the southern summer could have been counted as 188 days:
The creator of the G text, however, evidently described the star positions as they could be seen by a viewer at the time of rongorongo:
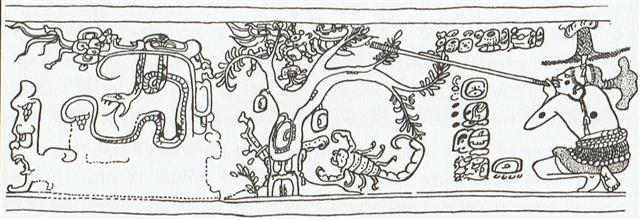
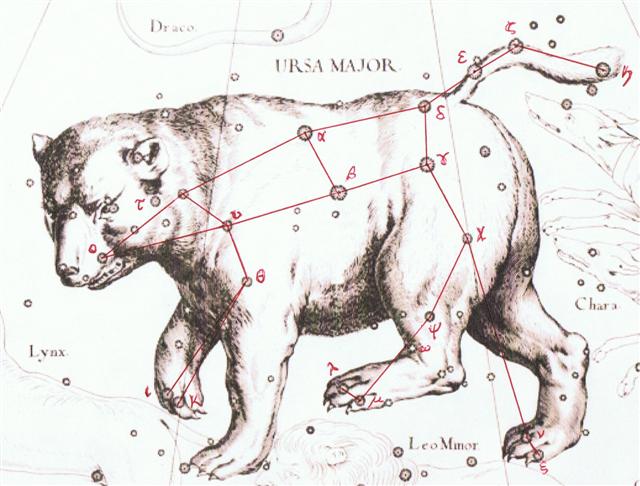
Thus Aldebaran was rising with the Sun in May 28 = 64 days after the Julian spring equinox. And according to the Mayas the defeat of vain-glorious (cfr Wain for Ursa Major) Seven Macaw also occurred in May 28:
... The modern dates counted from the site of Mayan Koba have been worked out from our modern Gregorian calendar and therefore it is possible to extrapolate backwards in time accordingly:
Seven Macaw had alighted in the top of the Tree - but a stone from a blow-gun had shot him down:
... This pot depicts one of the Hero Twins (One-Ahaw in the Classic texts and One-Hunaphu in the K'iche' Popol Vuh) and a great bird who is trying to land in a huge ceiba tree heavy with fruit. This mythical bird is Itzam-Yeh, Classic prototype of Wuqub-Kaqix, 'Seven-Macaw', of Popol Vuh fame. In that story, in the time before the sky was lifted up to make room for the light, the vainglorious Seven-Macaw imagined himself to be the sun. Offended by his pride, the Hero Twins humbled him by breaking his beautiful shining tooth with a pellet from their blowgun. This pot shows One-Ahaw aiming at the bird as he swoops down to land in his tree. As Itzam-Yeh lands on his perch, the text tells us he is 'entering or becoming the sky'. This particular 'sky-entering' is not the one mentioned in the Palenque text. It is the final event that occurred in the previous creation before the universe was remade. Before the sky could be raised and the real sun revealed in all its splendor, the Hero Twins had to put the false sun, Itzam-Yeh, in his place. If the date on this pot corresponds to that pre-Columbian event, as we believe it does, then Itzam-Yeh was defeated on 12.18.4.5.0.1 Ahaw 3 K'ank'in (May 28, 3149 B.C.). After the new universe was finally brought into existence, First Father also entered the sky by landing in the tree, just as Itzam-Yeh did ...
The Hero Twins gave the primary order in time of the present creation, and accordingly the day when the Sun arrived to Easter Island in a way ought to have been when the Sun reached Antares, i.e. 181 days after Aldeabaran.
However, there were 8 more days before the position of MARCH 31 in the night sky would reach the Full Moon (Hotu):
According to Manuscript E the Sun King was named Hotu A Matua, and before Venus as morning star was returning to visibility she was absent from the sky during 8 nights. Probably we should count 72 * 4 = 288 at Ga7-24, where a 'fruit' is hanging down in front.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||