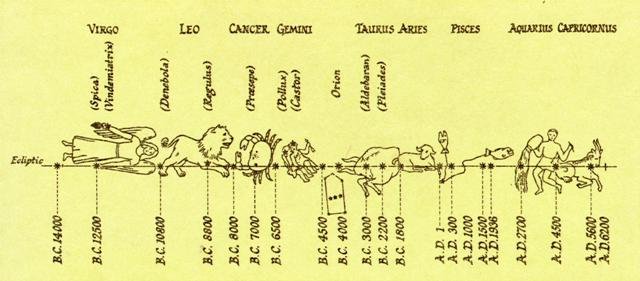
Once upon a time Aldebaran would have risen with the Sun in March 21 (our convention for the day of the northern spring equinox) and at that ancient time - it could be assumed - Antares would have risen around 181 days later in day 261 (September 18). Although the distances between the 'fixed' stars are not constant, but gradually changing due to their proper motions, such knowledge must have been hard to obtain and then to preserve in living memory. In reality the distance from Aldebaran to Antares had grown over time and in 5000 B.C. the distance from Aldebaran to Antares was around 177 (= 3 * 59) nights. This information can be gained from our modern time computer programs (e.g. Cartes du Ciel). From March 21 (day 80 counted from January 1) to May 28 (day 148) - when in rongorongo times Aldebaran rose with the Sun - there were 148 - 80 = 68 days. The stars which are 'fixed' onto the surface of our imaginary sky globe were rising later and later in the Sun year due to the precession, reflecting the way the Sun was reaching the northern spring equinox earlier and earlier among the stars:
The precessional measure 68 days can be derived from the illustration above (wich I have copied from the monumental work Hamlet's Mill. An Essay on Myth and the Frame of Time, composed by Giorgio de Santillana and Hertha von Dechend). In 3000 B.C. Aldebaran would have risen heliacally in March 21 and (3000 + 1842) / 26000 * 365¼ = 68.0, where I have guessed 1842 A.D. was the year which served as a point of reference for the rongorongo writers. And their conventional number of years for a complete precessional cycle could have been 26000 years. I have used the length of the year according to the Julian calendar - 365¼ days and slightly longer than the correct estimate - for calculating how many years were necessary in order to measure out 1 precessional day: 26000 / 365¼ = ca 71 years and (3000 + 1842) / 71 = ca 68 days. In the year 3000 B.C. the distance from Aldebaran to Antares would have been not 6 synodic months (as it had been 2000 years earlier) and not 181 nights (as it was in rongorongo times), but somewhere in between. We can easily find the approximate distance:
177 + 2000 / 6842 * 4 = ca 178.16 and therefore Antares would in 3000 B.C. have risen heliacally in day 80 (March 21) + 178 = 257 (September 14). I have made a table for finding the day number for a given date:
In 71 years a star would have changed its position with 1 day in the Sun year and this could hardly have gone unnoticed: The verdicts concerning the familiarity of ancient Near Eastern astronomers with the Precession depend, indeed, on arbitrary factors; namely, on the different scholarly opinions about the difficulty of the task. Ernst Dittrich, for instance, remarked that one should not expect much astronomical knowledge from Mesopotamia around 2000 B.C. 'Probably they knew only superficially the geometry of the motions of sun and moon. Thus, if we examine the simple, easily observable motions by means of which one could work out chronological determinants with very little mathematical knowledge, we find only the Precession.' There was also a learned Italian Church dignitary, Domenico Testa, who snatched at this curious argument to prove that the world had been created ex nihilo, as described in the first book of Moses, an event that supposedly happened around 4000 B.C. If the Egyptians had had a background of many millennia to reckon with, who, he asked, could have been unaware of the Precession? 'The very sweepers of their observatories would have known.' Hence time could not have begun before 4000, Q. E. D. (Hamlet's Mill)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||