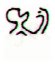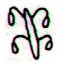|
The number of glyphs on side a of H can be considered to be 579 (580?), to be 648 (the sum of redmarked 627 and 21 in the table below), or to be 666 (= 648 + 18):
It has been shown that the burnt area probably was there already when the creator carved his glyphs on the tablet (cfr at hahe), but that anyhow 648 (= 6 * 108) is a good alternative. The visible glyphs on side a - including the vacant space for *Ha12-19 - sum up to the odd number 579, and maybe we should think '+ one more' as when we count to 472 glyphs for the text of G although there are only 471 glyphs on the tablet. 580 = 20 * 29. However, the burnt area covers also a space at the end of line a12 where an estimated number of 18 glyphs can be imagined. 666 (= 6 * 111) is therefore also a possible alternative. But neither 579 nor 580 is divisible by 6. On side b there is no burnt area. Yet, there are glyphs which are totally missing in line b1. There are 3 fully visible glyphs followed by 24 totally or partially invisible ones:
Then, suddenly, the glyphs are fully visible again. I guess those 24 more or less invisible glyphs are meant to be a sign. The redmarked 16 glyphs above are close to the 15 respectively 17 parallel ones in P and Q:
The picture of glyph line Hb1 in Barthel does not in any way suggest 16 must be wrong. Therefore we should calculate with *32 + 19 (*Hb1-33--51) = *51 glyphs in line Hb1 (while remembering to think ± 1). But we have two more question marks to consider, viz. in lines Hb8 and Hb12. There is a very special absent glyph in line Hb8 and it was discussed at hakaturou. The parallel text in P has here an unusual sign which I have decided to name pito (navel):
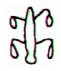
The creator of H has probably left a vacancy (clearly seen in the picture of the line in Barthel) for *Hb8-16. I have counted the vacant place among the *54 in the table above. The last question mark on side b needs a more detailed description. The uncertainty comes at the very end of line Hb12:
Maybe *Hb12-51 is a glyph which should be only imagined - like *Hb8-16. Or maybe we should accept that *Hb12-50 (where 12 * 50 = 600) is the last glyph of the text. In the latter case we can still reach 648 by increasing 51 to 52 in line b1:
And 52 (b1) + 48 (b2) = 100 seems to be equally good as 99. 413 = 14 * 29.5 instead of 412 for lines b1-b8 is better than 412. But then 648 - 413 = 235 suggests we should count also with *Hb12-51 in order to reach 236 (= 8 * 29.5). That decides it, I think, because 649 = 22 * 29.5 (and 22 suggests a full cycle because of the formula 22 / 7 = π). The ordinal number (counted from Hb1-1) of the glyphs at the end of line Hb12 will then be as follows:
In P, where all the glyphs are visible, the sums are 599 (side a) respectively 559 (side b). It could indicate a wish to end with 9 (here 99 respectively 59). Side a of G has 229 glyphs (excluding Gb8-30). The last visible glyph in H is Hb12-49, where 49 once again appears (in addition to in 649). Possibly it means a 'square of 7' is finished. 12 * 49 = 588 (= 300 + 288) and 6 * 49 = 294 (the final day before 10 * 29.5 = a 'zero' day is reached). I decide to change the tablet into:
Considering the sum of the glyphs on side a and side b the following alternatives are possible:
Mea ke in Hb6-29 should be an end glyph, and counting its ordinal number from Hb1-1 it becomes 284:
284 can be read as 2 * 84 = 168 (or maybe as 28 'in a square'). Counting from Hb1-1 seems to result in relevant signs. Both signs (168 respectively 28 and 4) should indicate that light is ending. Counting from Ha1-1 does also give more or less acceptable results:
None of these alternatives for side a can be excluded. If we should count with 649 glyphs on side b, then there will be 649 - 284 = 365 glyphs beyond Hb6-29. If we should count with only 50 glyphs in line Hb12 there will be 364 glyphs beyond Hb6-29. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||