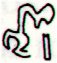
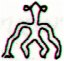
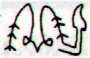531 is not a single sequence of glyphs, it consists of two different series, first 236 and then 295:
In G we can find 236 as:
9 + 9 'feathers' in Gb1-6 seems to say that half the cycle (472 / 2 = 236) has been reached. The full cycle will then be 472 = 16 * 29.5 glyphs long. Maybe the physical limits of the G tablet forced a shorter version of an otherwise standard 9 * 59 = 531 glyph long calendar with 4 doublemonths followed by 5 ('land' followed by 'fire'). Maybe the creator of the G text has added the missing 59 glyphs to the beginning of side a?
531 at Ga2-29 is here 472 + 59 (without adding Gb8-30 once more). The following manu kake will then be glyph number 532 - which can be read as 5 ('fire') times 32 ('days of growth') = 160 = 8 * 20 (or as 53 * 2 = 106):
It fits rather well. Each glyph can in G be counted as a day, and there will then be 300 days from manu kake to the end of the year:
5 lunar doublemonths of Sun are followed by 5 extra days ('one more' 5) in order to reach 300 days. The 'midnight henua' in Gb5-3 (as in 53) has a 'baby' hanging in front. Then follows 472 - 360 = 112 days to the end of side b and 59 at the beginning of side a. 112 + 59 = 171. But we must also add Gb8-30 and Gb5-2--6 in order to reach 3 * 59 = 177 days. Though still we have no more than 8 * 59 = 472 days in the calendar:
Hatinga Te Kohe could be at Gb5-1. It is at position 10 * 29½ counted from manu kake or at position 354 = 12 * 29½ counted from Ga1-1 (without adding Gb8-30). This kuhane station could indicate where the 'ruler' (old Sun) is 'breaking' - after 10 months according to what possibly was the old system or after 12 months acccording to a new system. There are two Vaitu months and two Hora months (cfr at honu): ... Whare-patari, who is credited with introducing the year of twelve months into New Zealand, had a staff with twelve notches on it. He went on a visit to some people called Rua-roa (Long pit) who were famous round about for their extensive knowledge. They inquired of Whare how many months the year had according to his reckoning. He showed them the staff with its twelve notches, one for each month. They replied: 'We are in error since we have but ten months. Are we wrong in lifting our crop of kumara (sweet potato) in the eighth month?' Whare-patari answered: 'You are wrong. Leave them until the tenth month. Know you not that there are two odd feathers in a bird's tail? Likewise there are two odd months in the year ... Conceptually 12 is clearly 2 more ('odd tail feathers') than 10 (the basis of counting in the 'decimal' system). But 12 may have been the basis of a more ancient 'duodecimal' system, where for instance 5 * 12 = 60. Also in Polynesia 12 months may have been there from the very beginning. The 'quality' of 10 is 'earth' (for instance because the kumara could grow for 10 months), whereas 12 has a 'flavour' of 'sky' ('fire', 5). The Moriori counted their years in groups of 12. They also used to divide their years into 12 months, or into 24 halfmonths if the women were counted (cfr at manu kake): ... the first month of the Moriori year, was named Rongo (Lono). On the first of the new year the Moriori launched a small canoe to Rongo, although they built and used only rude craft for their fishing excursions. The canoe was manned by twelve figures symbolizing the personifications of the twelve months. Sometimes twenty-four figures were placed in the canoe, and Skinner interprets the additional twelve as representing the female counterparts of the months. As an old Maori once remarked. 'Everything has its female counterpart ... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||