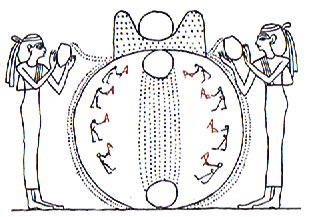
The fluids form double rows of 'droplets' (and the goddesses surely must represent the two faces of the moon). Each such double row is divided in two parts, a shorter part from the vessel to the mountain with double peaks and then a longer part from there to the bottom.

280 probably represents the number of nights moon is illuminated from the light of sun during 10 months or 20 fortnights. If we add 80 dots (inside the mountain with double peaks) we will reach 360.

The fundamental topological division into inside and outside has 128 + 106 = 234 dots on the inside of the central circle and 280 on the outside. To this must be added the dots inside the doublepeaked mountain. 234 + 80 = 314 is the number of dots inside either the central disc or the doublepeaked mountain.

Another possibility is to add the redmarked numbers: 128 + 280 = 408, which can be said to reflect 10 months with 32 days in each (because 40 * 8 = 320). This number apparently occurs as the ordinal number (counted from Gb8-30) of the last glyph before Rogo:

Gb6-25 (408)	Gb6-26	Gb6-27	Gb6-28	Gb7-1	Gb7-2	Gb7-3

The blackmarked 106 above will then, of course, be paired with those 80 inside the doublepeaked mountain: 106 + 80 = 186, which could indicate the 'nighttime' duration of the year. 18 * 6 = 108, a well known mythical number, and this can 'boil down' to 10 * 8 = 80. 108 + 300 = 408.

If we regard the standard year as 360 days (which the Egyptians did), then 360 - 186 = 174 = 6 * 29 = 464 - 290. If we instead count with 6 * 29.5 = 177 days for half a year, then 177 + 186 = 363 (the day of Rogo) = 354 + 9. 472 - 295 = 177.

The number of dots in the picture above are, though, hard to count with certainty. My numbers must therefore be considered as purely guesswork.