|
So far we have only an
interesting possibility, no 'proof' of anything. Next argument
is to point at the table below which 'proves' that 63 is not the
number to use, and that we should instead work with the much better 64 = 8
* 8, the square of the perfect number:
 |
61 |
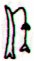 |
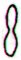 |
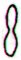 |
50 |
 |
|
Gb6-26 (1) |
Gb8-29 (63) |
Gb8-30 (64) |
Gb8-30 (65) |
Ga2-21 (116) |
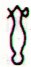 |
56 |
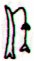 |
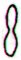 |
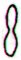 |
55 |
 |
|
Gb7-3 (1) |
Gb8-29 (58) |
Gb8-30 (59) |
Gb8-30 (60) |
Ga2-26 (116) |
Similarly it is 59 = 2 * 29.5 we
should use if we count from tamaiti (instead of from winter
solstice). The text of G is 472 glyphs long (1 more than the number
of glyphs on the tablet) and the natural glyph to
count twice is Gb8-30. That enables the reader to count 4 dark
months (4 * 29 = 116) from tamaiti (Gb7-3) to the beginning
of the henua calendar (Rei at Ga2-27). And ariki
at Ga2-21 marks the end of 4 dark months counted from honu at
winter solstice:
 |
114 |
 |
123 |
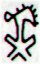 |
|
Gb6-26 |
Ga2-21 (52) |
Ga7-6 (176) |
|
116 = 4 * 29 |
124 = 4 * 31 |
|
240 = 8 * 30 |
The text of H is shorter (counted
in days) than the text of G and
it has an even number of days, 1296 / 3 = 432. Therefore we should not
try to count twice at the end of side b of H. |