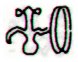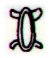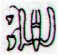In A we could at first try to transfer Aa8-24 from the end of Akahanga to the beginning of Hatinga Te Kohe, which would put a visible break at its beginning (equivalent to that between Gb4-33 and Gb5-1). But the expected number 708 (= 12 * 59) at Aa8-24 is 58 glyphs too low, and we need to adjust the point of beginning from Ab8-44 to Ab7-69 (100 glyphs from the end of side b):

Hatinga Te Kohe

12 * 29.5 = 354

 54
Aa8-24 (708) Aa8-25 Aa8-80 Aa8-81 Aa8-82 Aa8-83 (766)
60
99
Ab7-64 Ab7-65 Ab7-66 Ab7-67 Ab7-68 Ab7-69
40
Ab8-39 Ab8-40 Ab8-41 Ab8-42 Ab8-43 Ab8-44

Another possibility is to let Aa8-80 be the first glyph of Hatinga Te Kohe. But the counting should begin with pito (Ab8-43) for symmetry reasons - there are 84 glyphs in line b8. The logic is back - only after two glyphs in A can the same point be reached as after one glyph in G:

Hatinga Te Kohe  -  12 * 29.5 = 354
52
Aa8-80 Aa8-81 (708) Aa8-82 Aa8-83 Aa8-84 Aa8-85 Ab1-53 Ab1-54 (766)
354 355 356 26 383
30

Having to change side from a to b in the month of Hatinga Te Kohe in this version is an argument for choosing it (rather than to start counting from Ab7-59). We will therefore try it also with the earlier months (going backwards in time):

Akahanga  -  11 * 29.5 = 324.5
50
Aa8-22 Aa8-23 (650) Aa8-24 Aa8-25 Aa8-26 Aa8-27 Aa8-78 Aa8-79 (706)
325 326 327 25 353
29

29 days for Akahanga allows the 4 'nombres propres' (Aa8-18--21) to be in the same month:

Hua Reva  -  10 * 29.5 = 295
52
Aa7-47 Aa7-48 (590) Aa7-49 Aa7-50 Aa7-51 Aa7-52 Aa8-20 Aa8-21 (648)
295 296 297 26 324
30

Ihe tau in Aa7-48 now occupies the same position in the month as Aa8-23.

Te Pou  -  9 * 29.5 = 265.5
50
Aa6-72 Aa6-73 (532) Aa6-74 Aa6-75 Aa6-76 Aa6-77 Aa7-45 Aa7-46 (588)
266 267 268 25 294
29

Vai in Aa6-75--76 now have been transferred from Hua Reva to Te Pou.

Te Pei   -  8 * 29.5 = 236
52
Aa6-13 Aa6-14 (472) Aa6-15 Aa6-16 Aa6-17 Aa6-18 Aa6-70 Aa6-71 (530)
236 237 238 26 265
30

To complete we should also look at Roto Iri Are:

Roto Iri Are  -  13 * 29.5 = 383.5
50
Ab1-55 Ab1-56 (768) Ab1-57 Ab1-58 Ab1-59 Ab1-60 Ab2-29 Ab2-30(824)
384 385 386 25 412
29

The model is possible, but not convincing. It is still an open question from where the counting should begin. Let us therefore try to count from Ab7-69.