There
are 3 glyphs between the last of the viri (with
'cut-off' upper 'tail') and the pair Aa8-30--31:
|
3 |
 |
 |
53 |
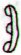 |
 |
520 |
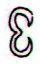 |
752 |
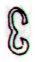 |
|
Aa8-30 |
Aa8-31 |
Aa8-85 |
Ab1-1 |
Ab7-26 |
Aa8-26 |
|
2 * 29 |
522 = 18 * 29 |
754 = 26 * 29 |
Counting from Ab1-1 we will find Aa8-31 to be glyph
number 1280. 521 + 754 + 5 = 1280. Aa8-31 is the 5th
glyph beyond the last viri.
Counting in groups of 5 (which is the natural way to do
it, using one hand to look at and the other to count
with), and in the beginning being restricted to simple
addition and subtraction, how do we reach such a large
number as 1280?
Before
true multiplication could be grasped indefinitely large
numbers could be reached by doubling. 1 seed of grain on
the first square of the chess board, 2 on the second, 4
on the third etc will within a short time lead to
astronomically large numbers.
Fact
is, the series 1, 2, 4, 8, 16, 32, 64, 128, 256 ... was
used for conveniently reaching large numbers. The
Mamari moon calendar has 8 periods and the 16th is
the last night of growing moon. 64 is the number of
squares on a chess board and 16 is also a square number
- square as the earth (which moon resembles).
256 is
also a square: 16 * 16 = 256. (All terms in the series
1, 2, 4, 8 etc which have odd ordinal numbers are
squares.) The 'earth year' - when sun is close instead
of being far away and the season is 'in the water' -
ought to be 256 days (like a 'great growing moon'
season). If we double the number of fingers on one hand
8 times we reach 5 * 256 = 1280. |
